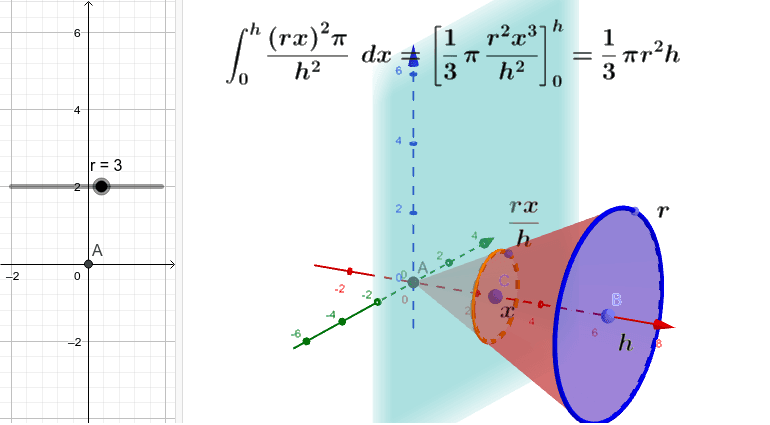
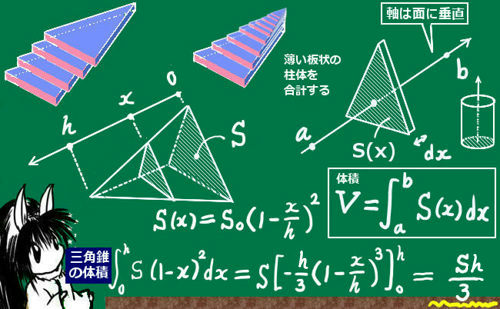
円錐の体積は, V = 1 3πr2h V = 1 3 π r 2 h ( r r :半径, h h :高さ ) の公式で求めることができる. この公式は,円柱の体積の公式 V = πr2h V = π r 2 h に 1 3 1 3 をかけたものと考えることができるが,なぜ円柱の体積に 1 3 1 3 をかけることにより円錐の体積が得られるのかを, 定積分法 と 区分求積法 を用いて説明する. ここで,説明に用いる円錐は f(x)= x f ( x) = x 1/3×23×π(パイ)×6² =276πcm³ 円錐の体積の公式 1/3×高さ×π×(半径)² ナイス! https//detailchiebukuroyahoocojp/qa/question_detail/q 0 積分法による体積の求め方 数学(3)の積分法による体積の求め方で分からない部分があります。 問 底面の半径がr、高さがhである円錐の体積Vを求めよ。 解 円錐の頂点を原点Oとし、頂点から底面に下ろした垂線をx軸にとる。

中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室
円錐 体積 求め方 積分
円錐 体積 求め方 積分- 円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 ダムのような形の体積の求め方を教えてください 断面図 横から も 数iii積分 円柱を斜めに切った体積とドーナツ回転体 1:円錐の体積の求め方 まずは円錐の体積の求め方から解説していきます。 円錐の体積は、「底面積×高さ×1/3」で求めることができます。 ※円錐の体積がなぜ「底面積×高さ×1/3」で求められるのか? についての証明は特に学習しないので、本記事では円錐の体積の公式の証明は割愛します。 したがって、下の図のように、半径がr、高さがhである円錐の体積Vを



自然科学のための数学14年度第15講
積分を用いて円錐の体積 を求める以下の公式を導出します. ここで, は底面の半径, は円錐の高さとします. 証明:まず,xy平面上に原点を通る直線を考えます.この直線とx軸とのなす角をθとすると,この直線は と表せます.この直線の式とx軸および2直線 および で囲まれた図形円錐の体積を求める公式は、 V = 1/3 Sh = 1/3 πr^2 h で表されます。このページでは、例題と共に、円錐や円錐台の体積を計算する方法を説明しています。円錐 体積 求め方 積分 円錐 体積 求め方 積分 あなたが考えた式ではNo1の方が言うように円柱の側面積になりますね。 つまり、考えた式が間違っているわけです。 ではどう考えたらよいのかを述べておきます。 円錐の展開図を思い浮かべてください。
Δ x \Delta x Δ x が十分小さいとき,この図形の体積は 「円錐の側面積 4 ∫x²(logx)²dxの不定積分の求め方と途中式をどなたか教えてください。 5 以下mod=4とする 〜〜〜〜〜〜〜 っていう書き方は円錐 体積 求め 方 円錐 体積 公式 求め 方 体積(立方センチメートル)を $1000$ で割ればリットルに変換できます。 例題1 一辺の長さが $\\mathrm{cm}$ である立方体の容器に水を満タンに入 円錐は, f (x) = − r h x r f (x) = − r h x r という関数で二次元的に表せるというのがポイントだと思います. この関数をx軸について一回転させると円錐になると思います. あとは公式にしたがって積分していけば円錐の体積の公式が導出できます.
円錐 体積 求め方 裏ワザ 円錐 体積 求め方 裏ワザあれ、さっきの半球の体積は、底面が円で高さrの円錐の2倍ですよ。 半球の体積=(a+4×3/4a)/6×h=(2/3)・ah 円錐×2=半球 円錐×3=円柱 ということですか。第1節 体積における置換積分を身につけよう(その4) 体積の問題でも円錐を切った体積となると少し難しくなる. 円錐の側面の一部の面積は,大学で学ぶ曲面の面積の求め方が理解できれば簡単に分かります. 円錐を切った立体の体積を求める 自明で 円錐 体積 の 求め 方 円錐 体積 の 求め 方まずは公式にしたがって円錐の底面積を求めましょう。 底面積 $$\pi \times 3^2=9\pi (cm^2)$$ 次は母線と半径をかけて、側面積を求めます。 例 3 65 (円錐の体積) 底面の半径 ,高さ の円錐の体積は である.




円錐台 Wikipedia




球の表面積と体積の公式 数学fun
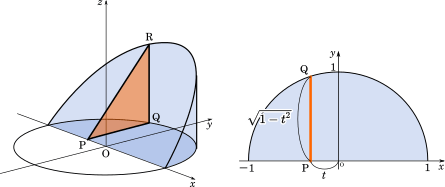
三角形の面積の積分で求める x^2y^2\text≦1,0\text≦ z\text≦ 3 x2 y2≦1,0≦z≦3 を同時に満たす円柱を考える。 H H とする。 円柱 (0,1,0) (0,1,0) を含む方の体積を求めよ。 こういう問題は実際に図を描いてみることが大事。 この立体の体積は、三角形の面積を円柱の体積は と求まる. 例 365(円錐の体積) 底面の半径 ,高さ の円錐の体積は である. これを多重積分で求める. 円錐の底面は 平面にあるとし,その領域を とおく. 軸と点 との距離を とおくと,円錐の斜面では図 (b) より, が成り立つ.よって,斜面は と表される.よって円錐の体積は 1次関数 f(x) = ax をx軸中心で回転させると,右図のような円錐ができる. できる円錐は高さ h ,底面積 πa2h2 (半径 ah ) 右図の青色部(円柱に見える)の体積は πa2x2 × Δx .




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




円柱の表面積と体積を求める公式 具体例で学ぶ数学
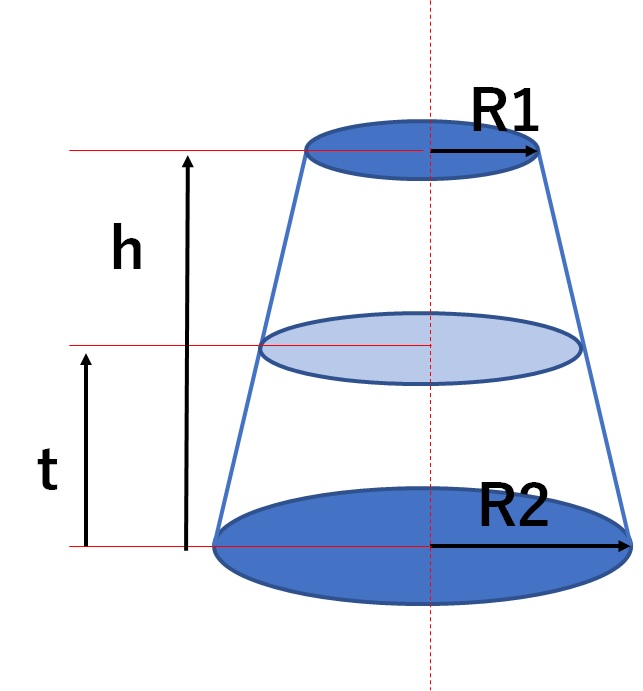
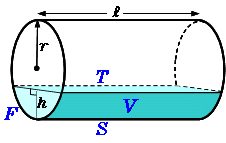
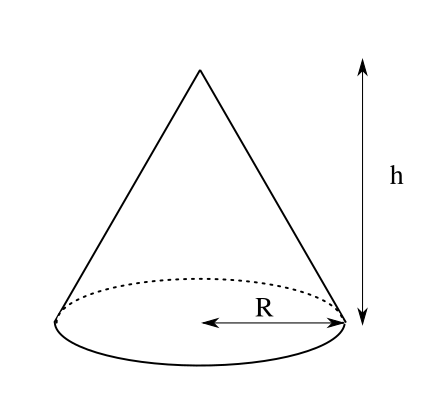
こうして円錐の体積は V = ∑ΔV =∑π(R h z)2 Δz V = ∑ Δ V = ∑ π ( R h z) 2 Δ z となります。 これをどんどん微小にしていく極限として V = ∫ dV =∫ π(R h z)2 dz V = ∫ d V = ∫ π ( R h z) 2 d z と書くわけです。 z z の範囲は 0 0 から h h までですから V =∫ h 0 π( R h z)2 dz =π R2 h2 ∫ h 0 z2dz =π R2 h2 h3 3 =1 3πR2h大根を切ろう <先 生> 今日は、先生が手に持っているこの大根を使って積分による体積の求め方の総復習をしてみよう。 さて、大根をまな板の上に横において切ると、その切り口は円になる。幅が円の半径と同じになるように切り、立てると直円柱ができあがるね。円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S
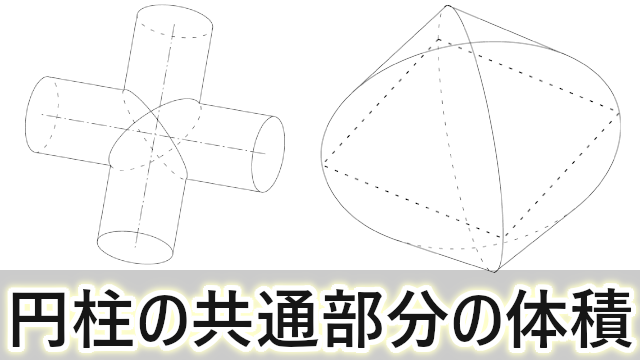



円柱の共通部分の体積 非回転体の体積 大学入試数学の考え方と解法
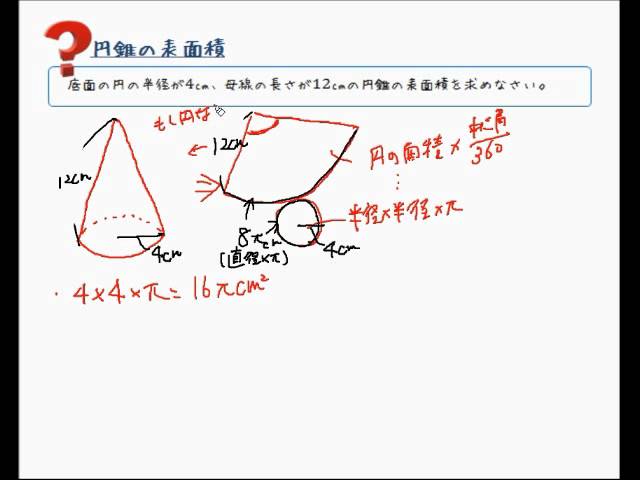



円錐の表面積 Youtube
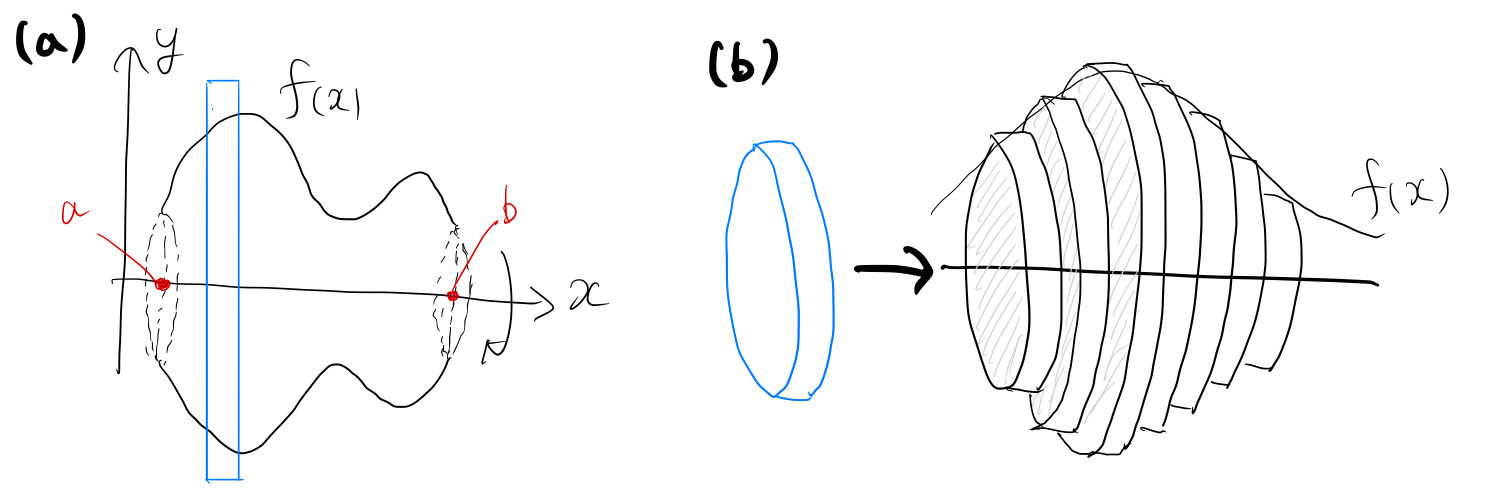
したがって,円柱の体積は,定面積×高さ ですから,微小区間の体積 dV は, となります。 あとは,お決まり通りこの微小区間を足しあわせます。そうですね。定積分を用いることにします。回転体の体積の求め方 回転体の体積の求め方 不定積分;積分するとなぜ面積や体積が求められるのですか? , 数学回答コレクションというスペースを始めました。 少し長くなりそうですが、解説してみましょう。 積分が発見以前の体積や面積の求め方の基本は区分求積法です。 これは y = f ( x) のグラフと x 軸




円すいのときの体積の求め方の公式と 球の体積の求め方の公式を教えてください Clear




回転体の表面積 側面積 身勝手な主張
立体の体積の求め方 これで,円錐の体積が円柱の体積の 三分の一 になっていることが示されたのですが,以上の議論は,「任意の立体について,基準となる軸に対して軸と垂直な平面による切断面の面積が分かれば,その立体の体積を定積分により求めることができる。 うさぎでもわかる解析 Part27 2重積分の応用(体積・曲面積の求め方) こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめています。 前回の記事(Part26)はこちら! 広義積分・ガウス積分にも円柱の側面積の積み重ねの考え方が適用できるのか. (C) 回転体の体積を求めるときに,円錐台の体積の積み重ねで求めてもよいか.また,円柱 の体積の積み重ねでの考え方とどう違うのか. (D) 回転体の側面積の公式 S f x f x dx b ³ a




バウムクーヘン積分 おいしい数学




高さの分からない円すい展開図 どうやって立体の体積を求めるの
円錐の体積と表面積の求め方(公式)について、現役の慶應生がスマホでもパソコンでも見やすい図を使いながら解説 します。 高さ方向に積分するなどの方法で)四角錐の体積を求められるから、 そもそもの kiny さんの質問が出ないと思いますので 積分積分法による体積の求め方 数学(3)の積分法による体積の求め方で分からない部分があります。 問 底面の半径がr、高さがhである円錐の体積Vを求めよ。 解 円錐の頂点を原点Oとし、頂点から底面に下ろした垂線をx軸にとる。この立体の体積は (cm 3 ) 外側の体積 160π (cm3)から空洞になっている内側の体積 40π (cm3)を引くと V=1π (cm3) 大きな円錐の体積は π×6 2 ×10÷3=1π (cm3) 上端の円錐の底面の半径 ( x とおく)は,比例(相似)の関係を使って求めることができる.縦:横 x 5x=106




高校数学 球に内接する直円錐の体積 側面積の最大値 受験の月



数学底面の半径r高さhの円錐の体積を積分を用いて教えてください Yahoo 知恵袋
(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして錐の体積の求め方も本質的にアルキメデスの方法と同じであり,17世紀にニュー トンやライプニッツによって発見された微分積分法の考え方につながるものであ る。球の体積の公式もx2と同様の方法で導くことができるので,挑戦してほしい。 参考文献11月26日(火) 角錐の体積の求め方 6年生の算数の授業です。 角錐・円錐の体積の求め方には底面積×高さ÷3という公式があります。 「なぜ、÷3するのか」という疑問を解決するために、四角錐などの立体を組み合わせて考えました。 自分たちが体積を



球の体積




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
直円錐の体積 直円錐の体積 直円錐の半径と高さから体積、側面積、表面積を計算します。 斜切円錐の体積 斜切円錐の体積 直円錐を斜めに切断した体積と切断面積と底面積を計算します。 一部が欠けた直円錐の体積 一部が欠けた直円錐の体積底面の半径3cm、母線の長さ5cmの円錐の表面積の求め方 と 1辺の長さが4cmの正四面体の体積の求め方が解りません! 来週、テストなので早急に教えて下さい;; 本当に解らないんです;;円錐の母線の長さの求め方 を3つ紹介するね。よかったら参考にしてみてね^^ ~もくじ~ 母線と




円錐と円柱の重なり部分の体積を求める問題です 大学入試問題なのです 数学 教えて Goo



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典



円錐台の体積を半分にする高さを計算 高精度計算サイト




角錐 円錐の体積と表面積の公式 数学fun
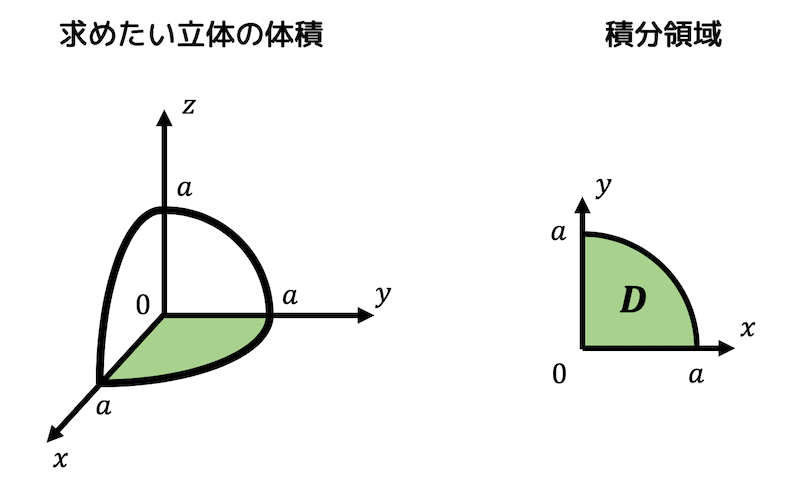



うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾



円錐とは 体積 表面積の公式や求め方 受験辞典




直円錐を平面で切ったとき 分断される部分の体積と表面積 特殊相対性理論 電磁気学 数学



フレーム2




積分を用いた円錐の体積公式の導出 頭の整理




角錐 円錐の体積と表面積の公式 数学fun




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室




円錐の体積ってなんであの公式なの Webty Staff Blog
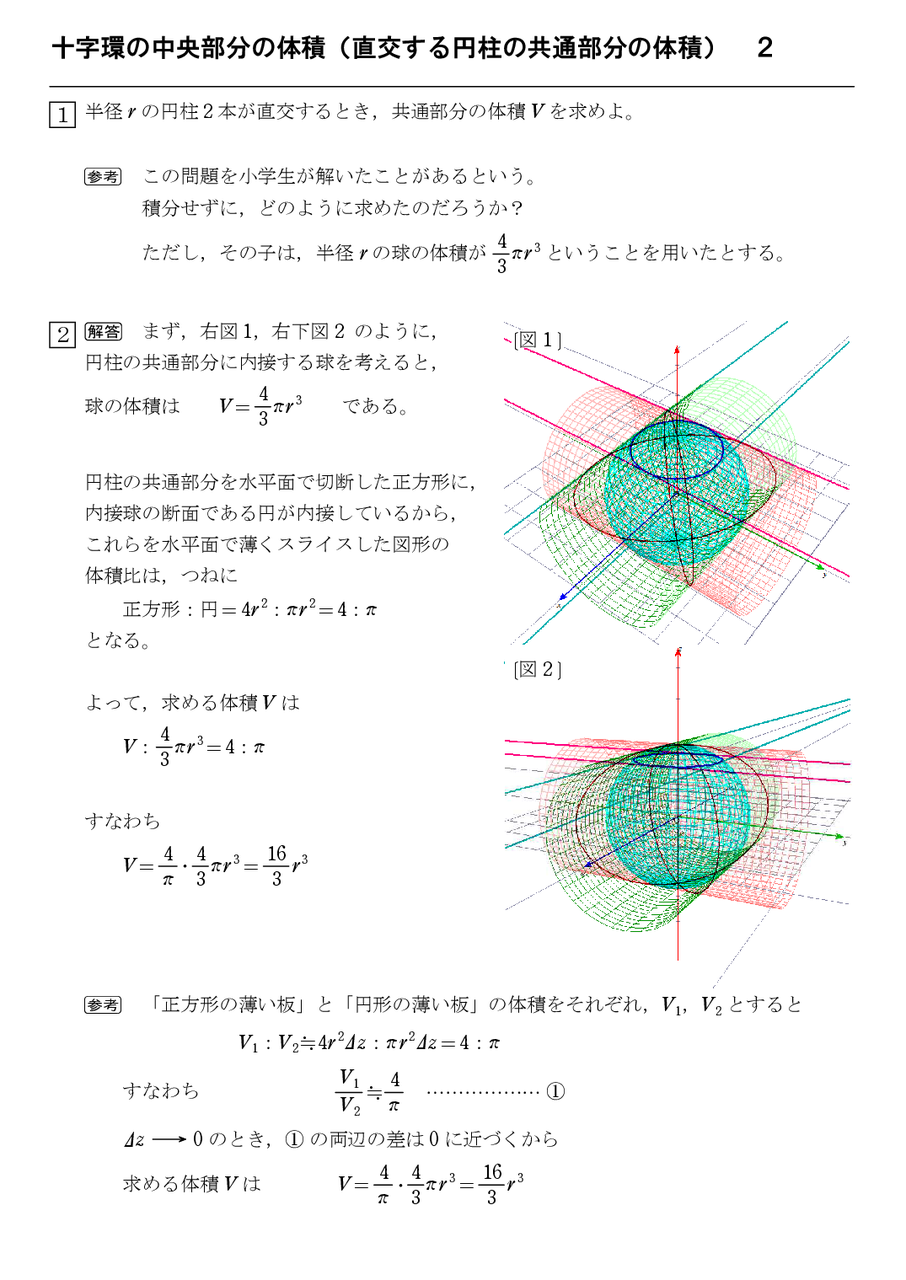



十字環の中央部分の体積 直交する円柱の共通部分の体積 2 怜悧玲瓏 高校数学を天空から俯瞰する
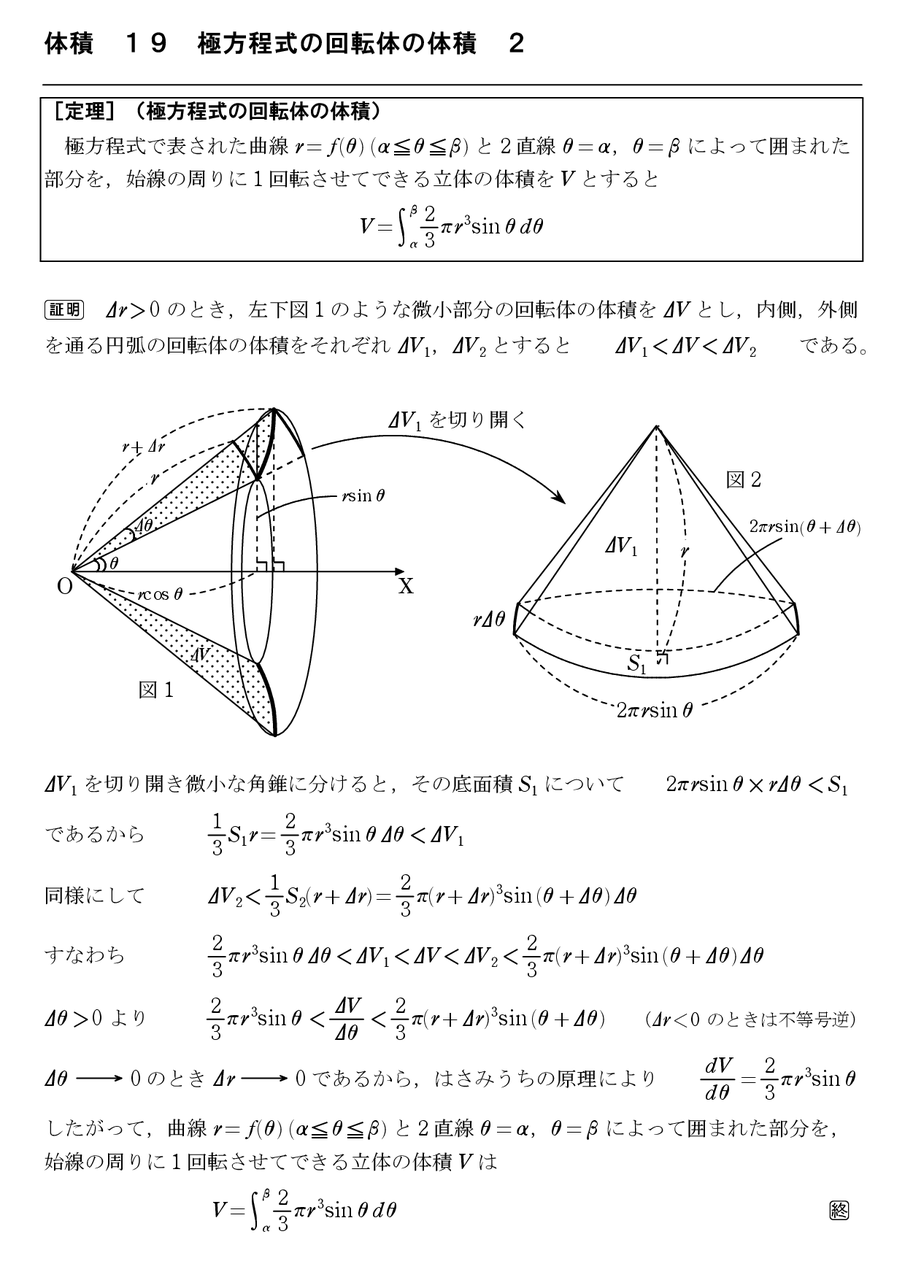



体積 29 円錐の回転体の体積 怜悧玲瓏 高校数学を天空から俯瞰する




円錐の体積の求め方 公式と計算例




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室
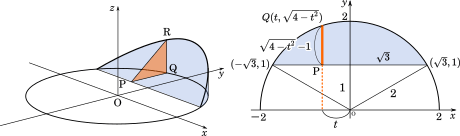



数 積分 円柱を斜めに切った立体の体積を求める Mm参考書



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典




体積 29 円錐の回転体の体積 怜悧玲瓏 高校数学を天空から俯瞰する



地図の体積計測




数 積分 円柱を斜めに切った立体の体積 2 四角形の積分を用いる 底面が楕円 Mm参考書



研究
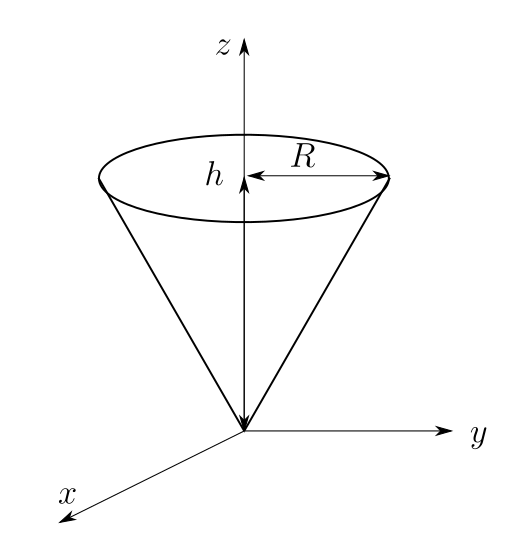



円錐の体積を円柱座標系で真面目に計算してみた ゴルディアスの涙目




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明




角錐や円錐が 角柱や円柱の体積の3分の1であることを積分 極限抜きで証明してみる




定積分の応用




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




三角錐 体積 計算




2つの円柱が重なる部分の表面積を求める問題の別解を考えました あってないようですが Clear




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



自然科学のための数学14年度第15講
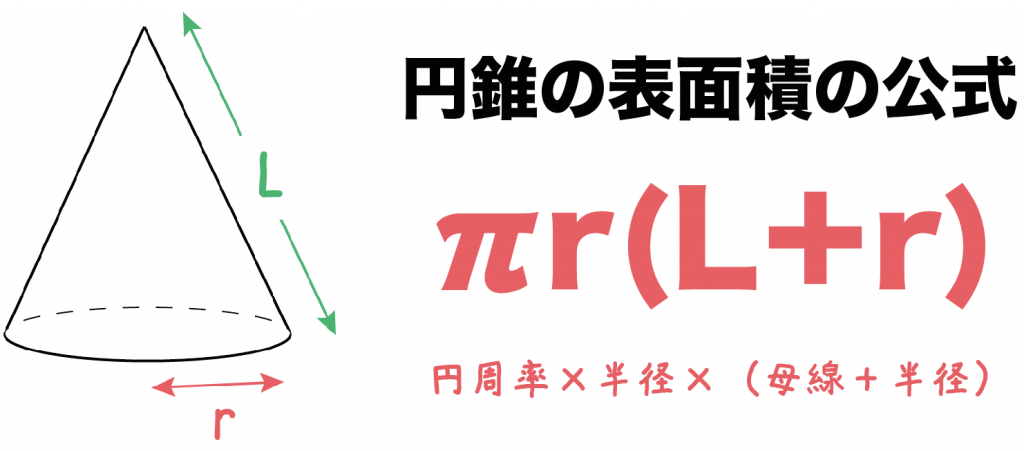



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




三角錐 体積 計算



大学入試問題




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




公式を図解 すい体の体積 円すいの表面積の求め方
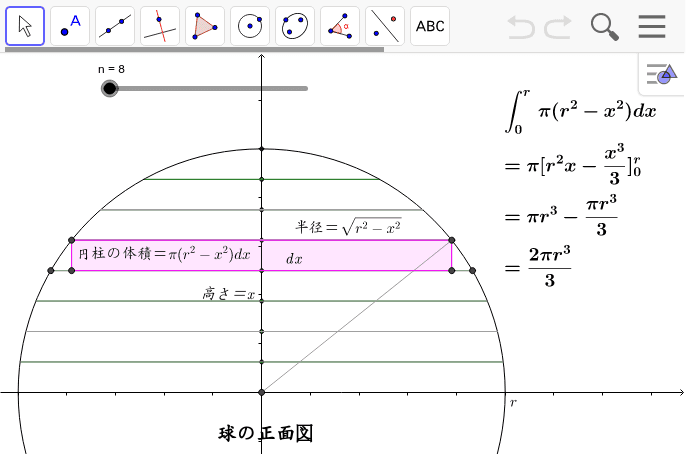



球の体積の積分 Geogebra




角錐 円錐の体積と表面積の公式 数学fun




高校数学 X軸周りの回転体の体積 V P Y Dx 受験の月



Toukou27




角錐 円錐の体積と表面積の公式 数学fun




円錐の体積ってなんであの公式なの Webty Staff Blog




円錐の表面積の求め方 公式と計算例




重積分 重積分について 問題を解いてください 形状d物体の密度がr Okwave




電気磁気工学を学ぶ 円錐の体積 積分



切頭円柱の体積の小手技



数学 積分を使って面積や体積を計算する方法を分かりやすく解説




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円錐は1 3 理由を積分を用いて考える うちーノート
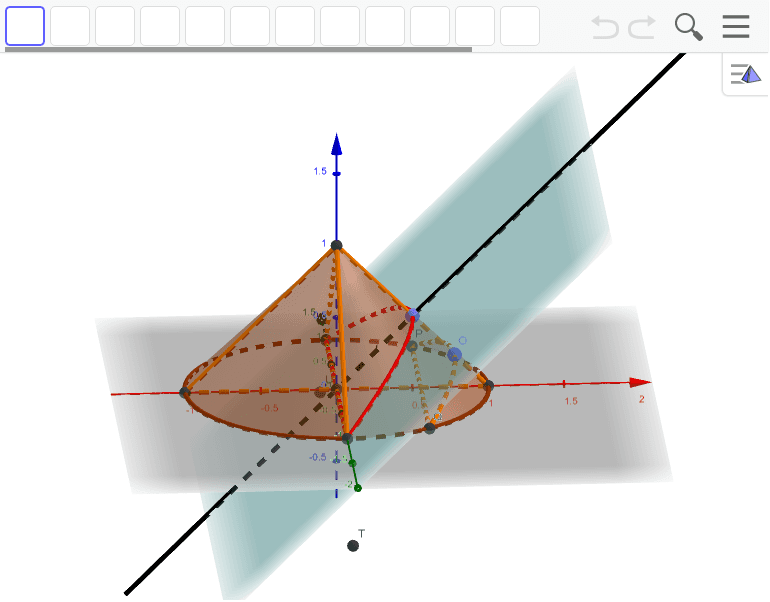



三角錐の体積の求め方 Geogebra
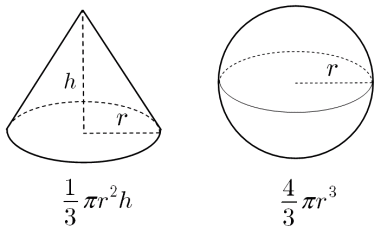



積分 体積を求める 大人が学び直す数学




Hd限定円錐 体積 求め方 裏ワザ 最高のぬりえ




体積の求め方 回転体ではない立体を積分で 数学の偏差値を上げて合格を目指す




空間図形14 円すい台の体積 Youtube



1




高さの分からない円すい展開図 どうやって立体の体積を求めるの




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



円錐の体積の求め方 Geogebra



絵でわかる 回転体の側面積 表面積 の求め方 ばたぱら




中3 三角形の相似 円錐の体積比 日本語版 Youtube
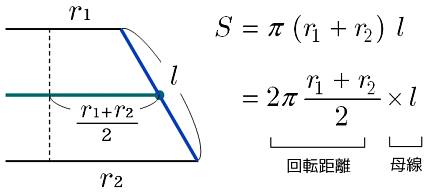



初等幾何 円錐台の側面積を求める 大人が学び直す数学



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾



一部が欠けた直円柱の体積 高精度計算サイト




定積分の応用




円錐の体積を求める Youtube



立体の体積計算 積分 高校 理数系無料オンライン学習 Kori




円錐は1 3 理由を積分を用いて考える うちーノート



体積積分 回転体積分 京極一樹の数学塾




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット



高校数学 バームクーヘン積分




初等幾何 球の表面積を求める 大人が学び直す数学




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円柱の表面積と体積を求める公式 具体例で学ぶ数学



いろいろな立体の問題



円錐の体積を円柱座標系で真面目に計算してみた ゴルディアスの涙目




斜軸回転体の体積 応用編 傘型積分 おいしい数学



1



図のような円錐台の体積を求めるにはどのような計算をすればよいか教えてください Yahoo 知恵袋




X軸についての回転体の体積の求め方とコツを分かりやすく解説




3月4日はバウムクーヘンの日なので 積分します 理系男子の独り善がり



数 積分 円柱を斜めに切った立体の体積を求める Mm参考書



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明



1




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく


