一次関数とは「y=axb」で表される式のことです。 文字ばっかりで勉強したくなくなりますね。 おまけに変化の割合、傾き、変域なんていうよく分からない単語まで出てきます。 ただでさえやる気がでない、集中が続かないのに単語まで難しいと「ノー勉でもいいや」と思ってしまうかも (「関数」の主役が y だとしたら、「方程式」の主役は x 、といったようなイメージでしょうか) 例えば、一次関数 y = 2 x 1 があり、 y = 4 となるような x を求めたいときは 2 x 1 = 4 という方程式を解くことになります。 一次関数の式「y = ax b」に傾きaと、座標を代入してやればいいんだ。 bの方程式ができるから、そいつを根性でとくだけさ。 例題では、 傾き:3;
一次関数と方程式 の記事一覧 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
一次関数と方程式 解き方
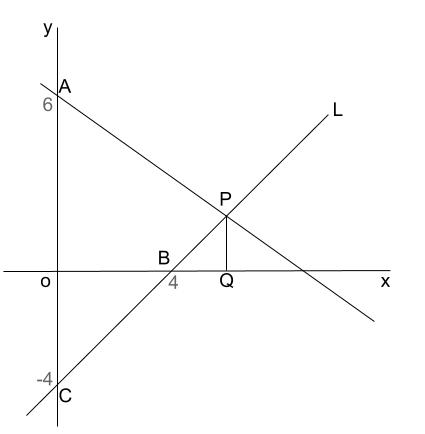
一次関数と方程式 解き方-ウ 二元一次方程式を関数を表す式とみることができること。 評価の観点 数量,図形などについての知識・理解 下の図で,直線 は方程式 + =5のグラフ,直線 は方程式 - =1のグラフです。 ア 点 イ 点数学、特に初等解析学における(狭義の)一次関数(いちじかんすう、英 linear function )は、( 一変数 (英語版) の)一次多項式関数( firstdegree polynomial function )、つまり次数 1 の多項式が定める関数 ↦ をいう。( もしくは = と表記される)ここで、係数 a (≠ 0), b は x に依存しない定数



一次関数 グラフの書き方 苦手な数学を簡単に
二元一次方程式とは、文字が2文字で、文字の掛け合わせがない方程式でしたね 例えば、 x2y = 3 などですね ( 〇元〇次の意味) 二元一次方程式は、yの式(左辺がyだけの式)にすると、「1次関数」ですね よって、① yの式にする → ② 1次関数として扱う それこれで連立方程式は解けました。 最後に「答え方」ですが、 これは「直線の式」を求める問題なので、 "y=ax+b" の形で 答える必要がありますね。 a=-2 、 b=12 ですから、 y=-2 x+12 (答) これで満点です! <まとめ> 1次関数の式を求める問題で、数学23章一次関数 「二元一次方程式と関数」<基本問題①> 組 番 氏名 次の問いに答えなさい。 (1)次のア~エの中で,二元一次方程式3χ-y=8の解になるのはどれですか。
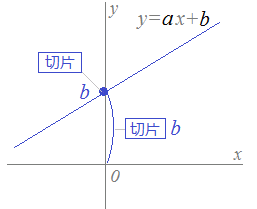
イ 一次関数について,表,式,グラフを相互に関連付けて理解すること。 ウ 二元一次方程式を関数を表す式とみること。 エ 一次関数を用いて具体的な事象をとらえ説明すること。 学習指導要領の内容項目C関数(1)一次関数の式は? 一次関数の式は、『y=axb』という式で表せます。この式は何を表しているかというと、 直線になる、ということです。 比例のところで、比例の式はy=axで、原点を通る式になる、ということを習っていると思います。2点から1次関数の式を出す方法は2通り。 ① 変化の割合を出し、傾きと1点から式を出す。 ② x,yをそれぞれy=axbに代入して連立方程式にしてa,bを出す どちらの方法でも1次関数の式が出せる。
1、一次関数とは何か (1)yがxの関数で、yがxの一次式で表わされるものを一次関数という 最初にいくらかの量があり、それから決まった割合で増えていく2つの量があるとき、2つの量の関係が一次関数である (例)水が5L入っている水そうに毎分2Lの割合で水を入れるとき、水を入れ始めてからx分後の水そう中の水の量をyLとする 最初の量が5で、毎分2ずつ増え続ける方程式 2進法 k社 2次関数 二元一次 不定方程式 二進法 t社 2次関数 2元1次 方程式 2進法 d社 2次関数 2元1次 方程式 二進法 j社 2次関数 二元一次 不定方程式 2進法 何と,学習指導要領は,すべて漢数字使いである. また,教科書会社5 社とも「2 次関数」である2点を通る直線の方程式 切片を用いた直線の方程式 2直線の交点の座標 3点の座標で囲まれる三角形の面積 座標点で囲まれる多角形の面積 座標の回転 座標軸の回転 直交座標から極座標へ変換 極座標から直交座標へ変換
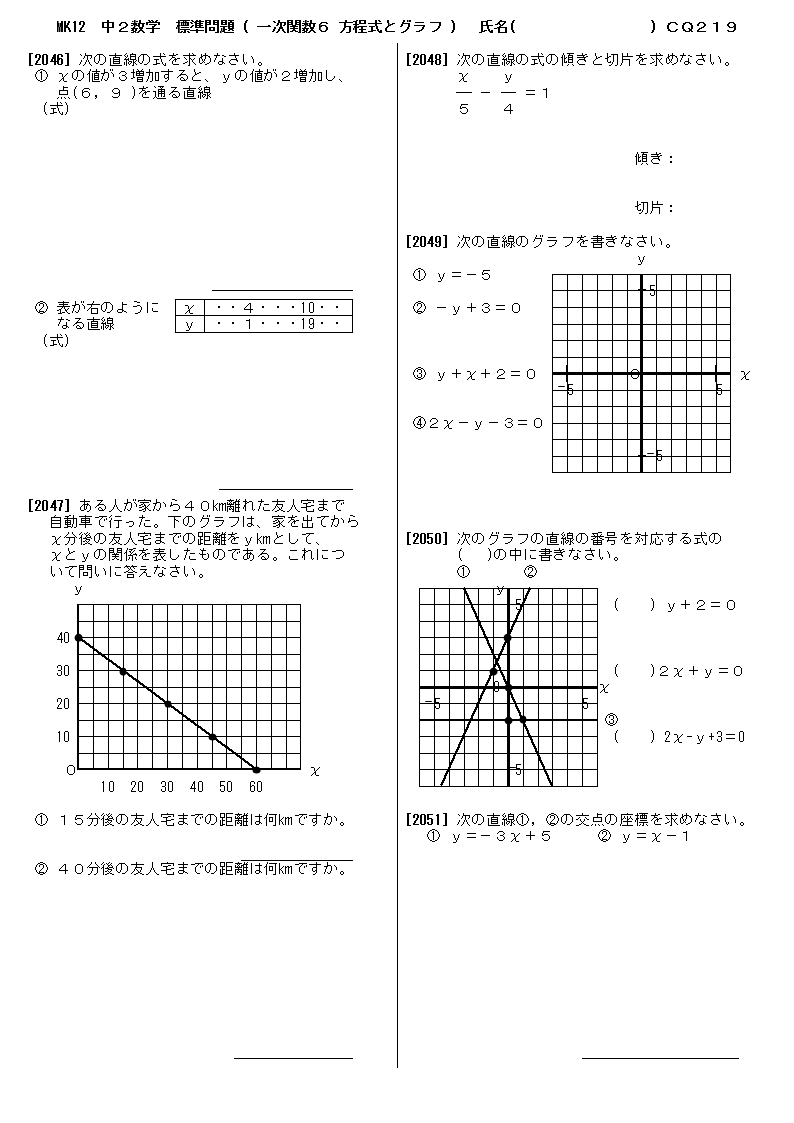



無料 中2数学 標準問題 問題プリント 219 一次関数6 方程式とグラフ



一次関数と連立方程式 1 ネット塾
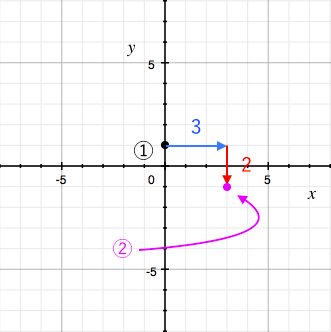
2方程式と一次関数4・二元一次方程式のグラフの意味や連立方程式の解と 本時グラフとの関係を理解する。 ()2/4 33章のまとめ1・一次関数の意味、変化の割合、一次関数のグラフ、 直線の式の求め方、二元一次方程式とグラフのまとめ をする。/1/7 2年一次関数総合問題Lv3 5 (2) 点Pはlとx軸の交点 (誤)→点Bはlとx軸の交点 (正) 3年方程式文章題 (割合2)3 (1)解答 2番目の式 yの係数 97 100 (誤)→ 93 100 (正) 7 3年2乗に比例する関数総合問題4 5問題 点A, P, Qを頂点とする (誤)→点D, P, Qを頂点とする座標(2, 10) っていう一次関数だったよね?? まずはaに傾き「3」を代入してみると、 y = 3x b になるでしょ?




一次関数 式の求め方をパターン別に問題解説 数スタ




一次関数はこれで完璧 グラフの書き方と変化の割合の求め方
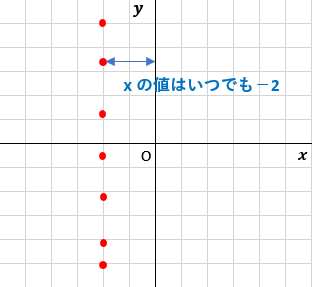
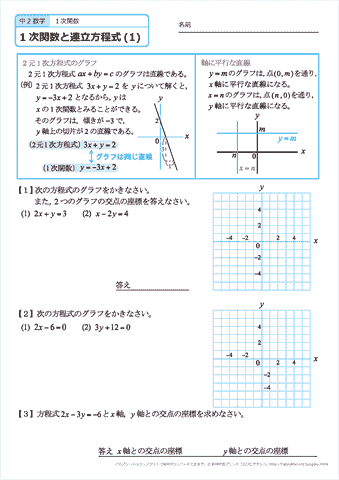
一次方程式の解 110 /17件 表示件数 5 10 30 50 100 0 1 1845 男 / 歳未満 / 小・中学生 / 役に立たなかった /14 一次関数と方程式 78 3章一次関数 確認問題1 次の方程式のグラフをかきなさい。 ⑴ xy2=0 ⑵ 3xy=1 ⑶ 2x3y6=0 ⑷ 3x2y=5 5 5 5 5 x y O 確認問題2 次の方程式のグラフをかきなさい。 ⑴ y=5 ⑵ 5y10=0 ⑶ x=1 ⑷ 2x12=0 5 5 5 5 x y O 例題 方程式5x2y10=0 のグラフをかきなさい。 解 y について解くと,y= 5 2 x5 だから,傾き 5 2 ,切片 5 のグラフをかく。第6節 1次関数と方程式 ☆ 1次関数は式を用いて表されました。同じように式を用いるものとして方程式を学習し ました。ここでは関数と方程式の関わりについて調べていきましょう。 (1)2元1次方程式 2元1次方程式 2xy=7 で、xが次の値のときにyの値を求めてみましょう。




切片が分数の時どうやってグラフを書くのかがわかりません 教えて欲しいです Clear




一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく
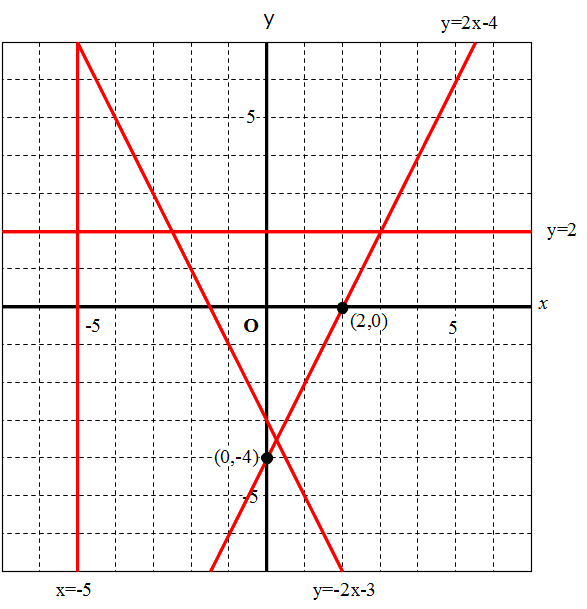
直線の方程式(一次関数)はy=ax+b (a,bは定数)で表わされます。 (※y軸に平行なものを除く。) 2点を通る直線の方程式を求めるには,2点のx,y座標を直線の方程式に代入して,定数a,bの連立方程式を解きます。 例題1二元一次方程式と一次関 数の関係に気づかせるた めに,二元一次方程式と 一次関数の両面から解決 できる問題場面を設定す る。 技:具体的な場面を利用して,二元 一次方程式と一次関数を同定 しようとしている。 (発言・プリント分析)一次関数の式にそれぞれ当てはめてやれば完成です。 傾き5を a の部分に、切片-2を b の部分に当てはめてやると 答えは\(y=5x2\)となります。
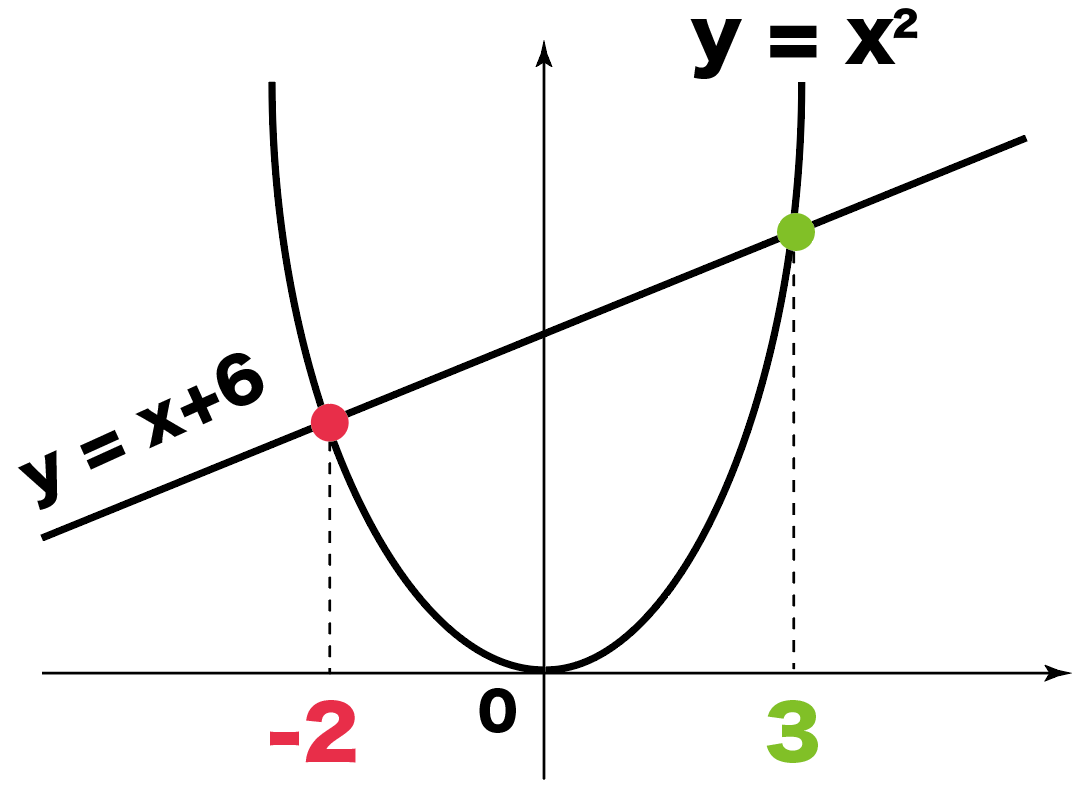



一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
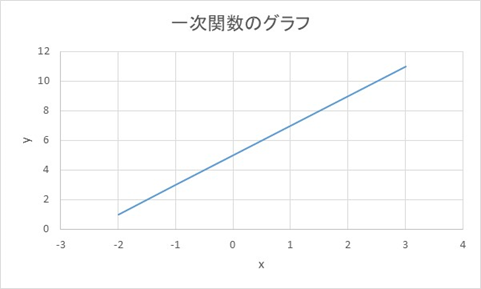



Excel エクセルにて1次関数 一次方程式 の計算 解や傾き とグラフ化の方法 複数も More E Life
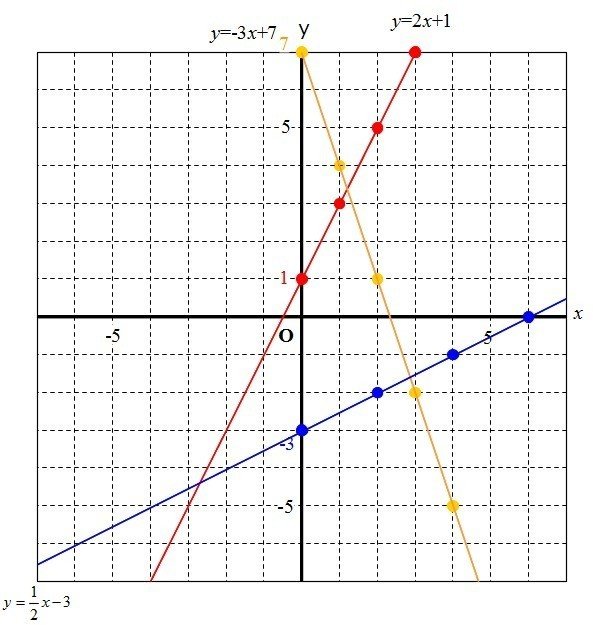
平面の方程式、法線ベクトル 設定 幾何ベクトルの空間を公理的に設定しておくべきだけども、 省略。 平面上の幾何ベクトルの説明→岡田『経済学・経営学のための数学』21(p567) 空間上の幾何ベクトルの説明→佐武付録、斉藤付録一次方程式 (一元一次方程式) ア 方程式などの意味 「 方程式 (ほうていしき)」・・・何か言葉だけで威圧されてしまいますね。 ですが、構える必要は全くないです。 順を追って説明しますね 《 例 》 3x2=8 という式があるとします。右の直線の傾きは 1 です. 直線の方程式は y= 1 xb=xb の形になります. 切片 b=2 も読み取ると,結局,直線の方程式は y=x 2 であることが分かります. ②のグラフは x の正の向きに1目盛り進んだときに y の向きに 2 だけ進んでいるので,直線②の傾きは 2 です. 例5 右の直線の傾きは 2 です( a=2 ). 直線の方程式は y= 2 xb の形になります. 切片 b=1 も




一次関数のグラフ 傾き 切片が分数 グラフの書き方を徹底解説 数スタ




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
一次関数も一次方程式もどちらもグラフが直線になりますよね? 一次でも、二次でも、関数 f(x) に対して等式 f(x)=0 が(一元)方程式です。 文字を増やして y=f(x) とすると、(二元)方程式に 一次方程式の解き方 ここからは、一次方程式の解き方を解説します。 一次方程式を解くには、4つのSTEPが必要になります。 例題を元に詳しく見ていきましょう!一次関数のグラフ( 一次関数のグラフのまとめ~グラフの書き方) 一次関数のグラフ(式の求め方) 一次関数 と方程式 連立方程式 とグラフ 一次関数の利用1 一次関数の利用2(動点の問題) 二学期中間
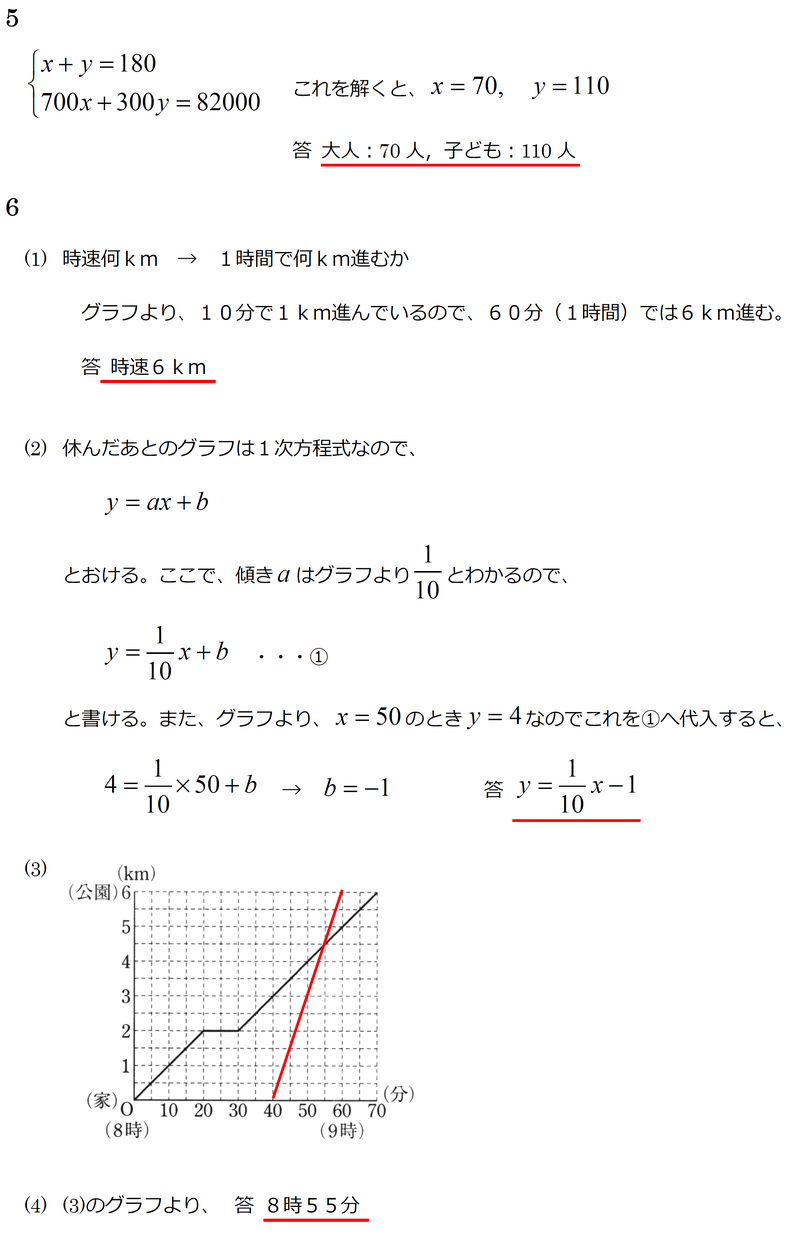



中学 数学 実力テスト 過去問 連立方程式 1次関数の利用 問題と解答 赤城 ᐡᐤᐡ
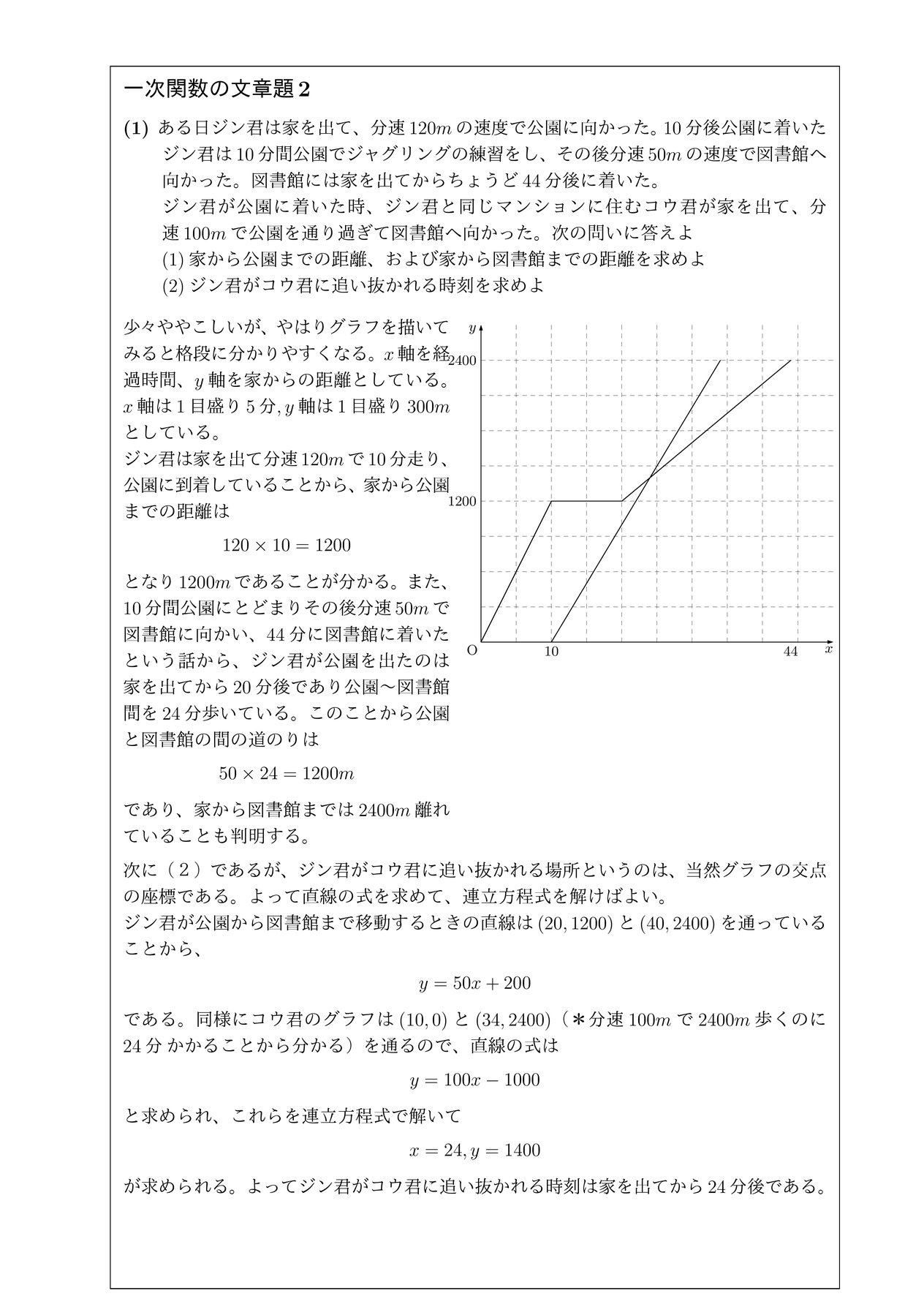



一次関数の文章題 道のりと時間 チーム エン
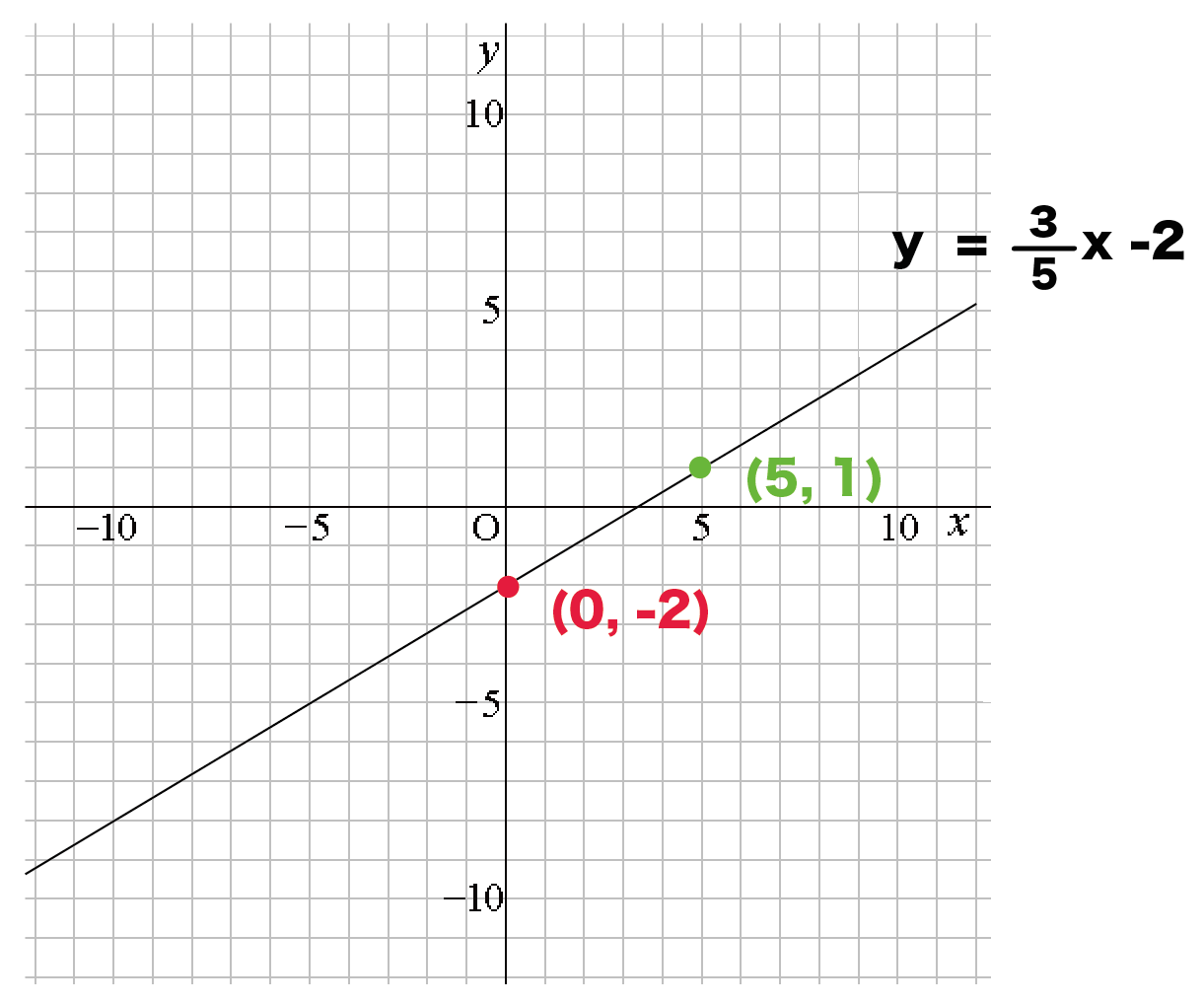
1次方程式と1次関数の関係 y = 3 2x − 2 のグラフ 1次関数 y = 3 2x − 2 において、このグラフと x 軸との共有点を考える。 共有点の y 座標は 0 であるから、共有点の x 座標は 3 2x − 2 = 0 という1次方程式の解として求めることができる。 この方程式の解は、次のような式変形を行い 3 2x − 2 = 0 ⇔ 3 2x = 2 ⇔ x = 4 3 と求めることができる。 つまり、 y = 3 2x − 2 のグラフと一次関数と方程式(式を求めること) 氏名( 解 答 ) 1 次の一次関数の式を、それぞれ求めなさい。 (1) グラフが、直線y= 1 2 x+1に平行で、点(-2,2)を通る直線 y= 1 2 x+3 (2) グラフが、点(-1,0)を通り、切片-1の直線である。注意:例えば, sin x \sin x sin x は 0 ≤ x ≤ π 2 0\leq x\leq \dfrac{\pi}{2} 0 ≤ x ≤ 2 π の区間で考えれば単射になる。 つまり,考える定義域,終域によって全射性,単射性は変わってくる。以下で扱う関数方程式の文脈では,多くの問題で定義域と終域が一致しており,実数全体または有理数全体と




中2数学 1次関数 3 2 連立方程式とグラフ Youtube




中学3年 数学 実力テスト 期始めテスト用問題 1次関数と2次方程式の利用 赤城 ᐡᐤᐡ
☆一次関数の表,式,グラフの相互の関連をまとめ,理解を深める。 2 一 次 関 数 と 方 程 式 (3) 節とびら c(1)ウ ☆二元一次方程式の解の値の組を座標とする点をとる活動から,二元一次方程式と一次関数の関係を見いだす。 2 1 方程式とグラフ一次関数の式に \(x=0\) を代入して計算していきましょう。 すると、交点の\(y\)座標を求めることができるので\(y\)軸との交点は $$(0, y座標)$$ とすることができます。 また、一次関数の式 \(y=axb\) の\(b\)部分を見ることですぐに求めることもできます。式の計算 魔方陣 カードゲームの得点 すごろくゲーム 数あてクイズ 不等式 上皿てんびんと身近な品物 上皿てんびんと押しピンの数 連立方程式 修学旅行の部屋割 中国の数学 一次関数 折り紙 正方形の積み上げ 図形の調べ方 魔方の円板




一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく
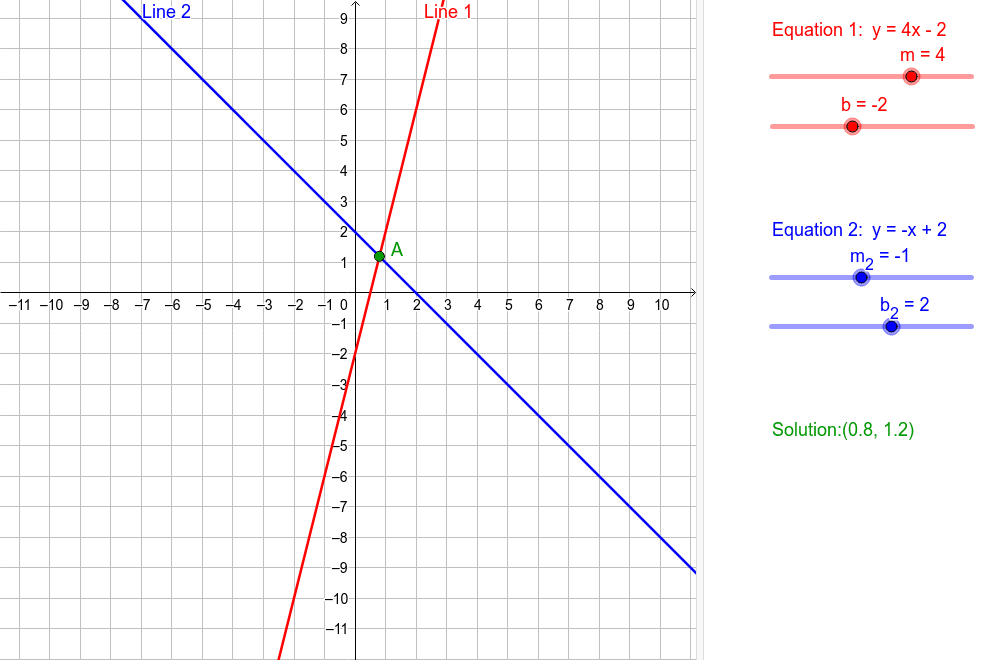



1次関数と方程式 Geogebra




中学2年生の数学 1次関数と正方形 長方形 塾講師が数学をやりmath




数学 中2 32 一次関数の式をもとめる 基本編 Youtube



1
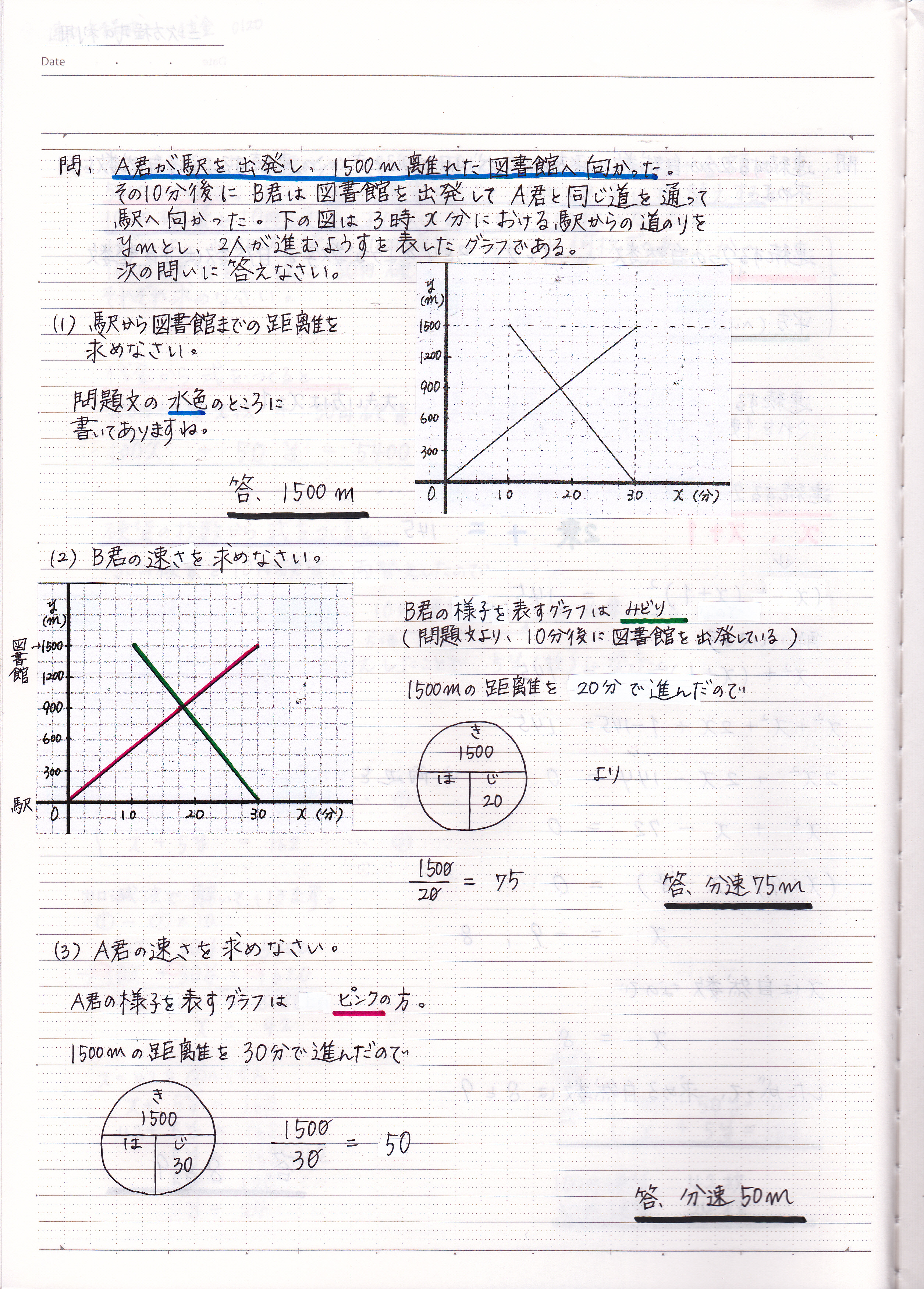



一次関数の利用の問題の解き方 速さ 3 現役塾講師のわかりやすい中学数学の解き方




切片とは 超簡単 切片を一瞬で求める方法 傾きとの違い 高校生向け受験応援メディア 受験のミカタ




一次関数の問題です Clear




一次関数と方程式 の記事一覧 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




課題学習の指導 数学



Http Www Juen Ac Jp G Katei Nunokawa Function 2 2 5 Pdf




一次関数の式を決定1 無料で使える中学学習プリント
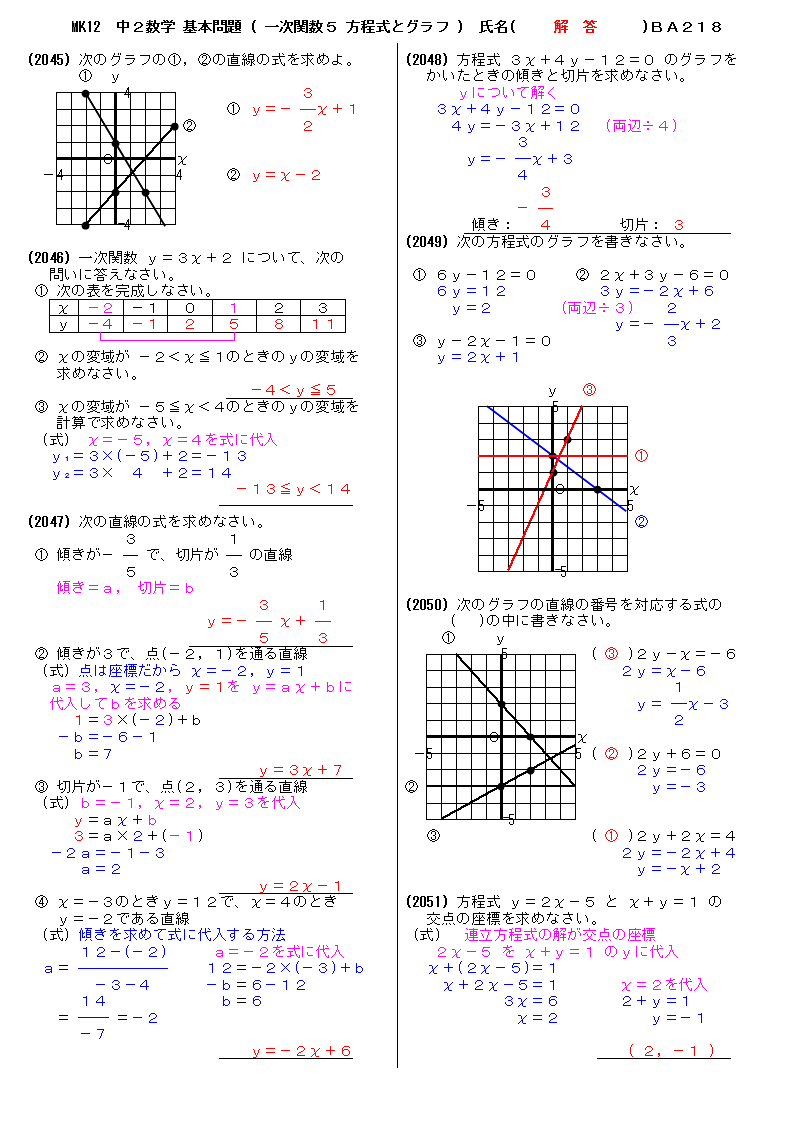



無料 中2数学 基本問題 解答プリント 218 一次関数5 方程式とグラフ




1次関数 2点を通る直線の式の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




一次関数と方程式 の問題 中学2年の数学 Okwave




一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく
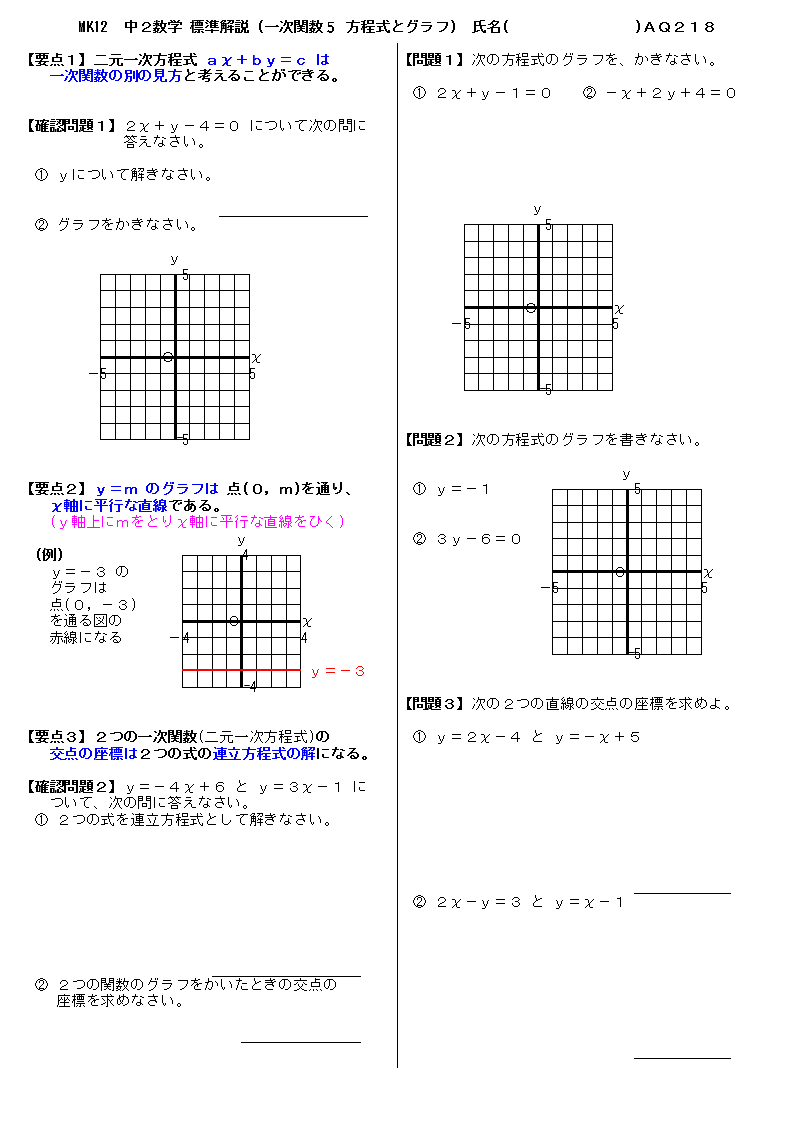



無料 中2数学 基本解説 問題プリント 218 一次関数6 方程式とグラフ




数学 一次関数 中学生 数学のノート Clear
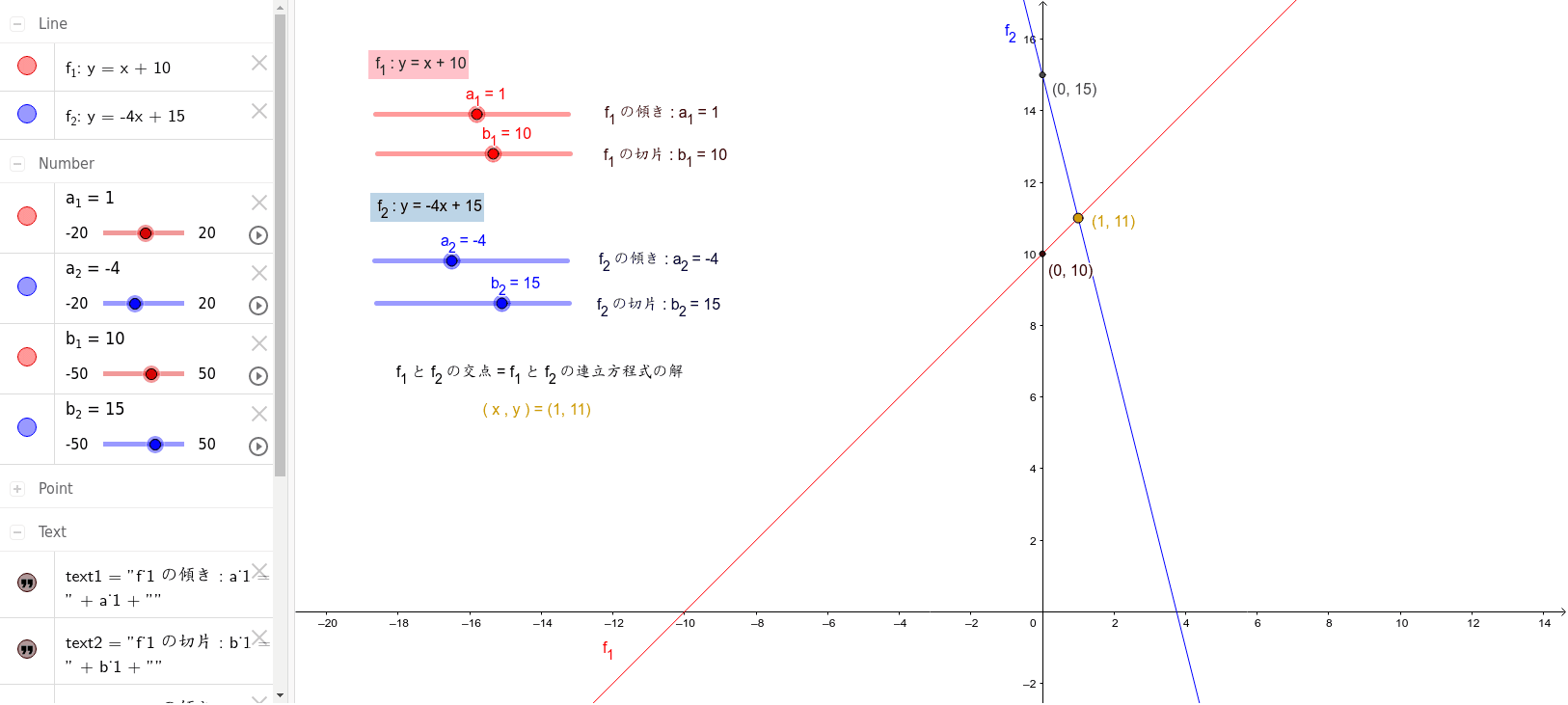



一次関数の交点と連立方程式の解 Geogebra




一次関数の問題の解き方 7パターン 数学fun




中2 方程式と一次関数の利用 中2の方程式と一次関数の問題ですが 添付 Okwave
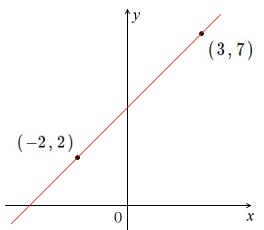



1次関数の交点の座標とグラフから直線の方程式を求める方法




一次関数 グラフの書き方 苦手な数学を簡単に
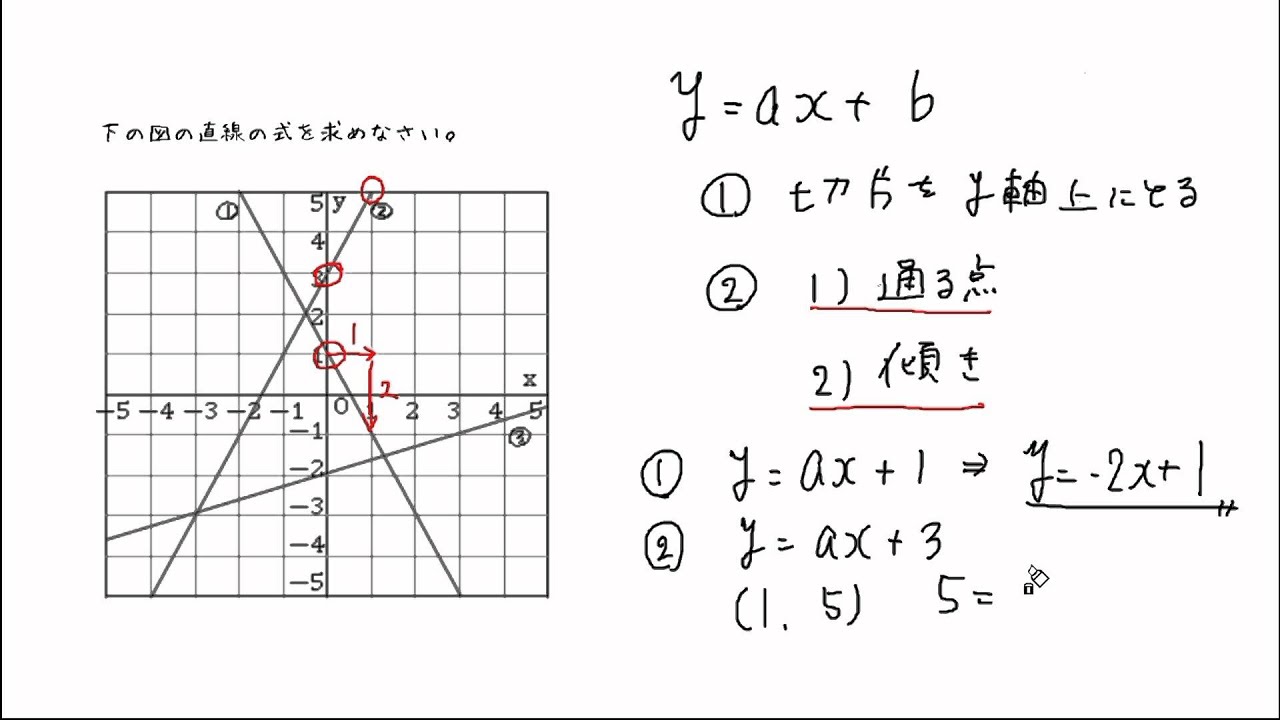



グラフから一次関数の式をもとめる Youtube
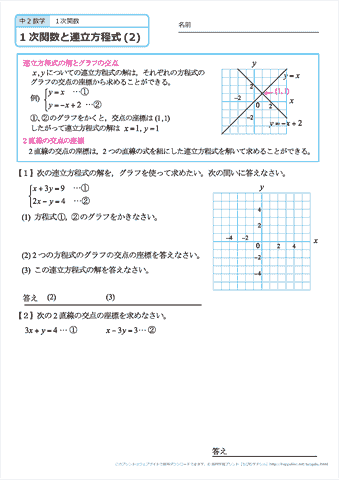



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




一次関数の傾きと切片を求める問題 Irohabook



1次関数と方程式 中学数学の無料オンライン学習サイトchu Su




二 点 を 通る 直線 ある2点を通る直線 一次関数 の方程式の計算方法 傾きと切片の求め方 Amp Petmd Com
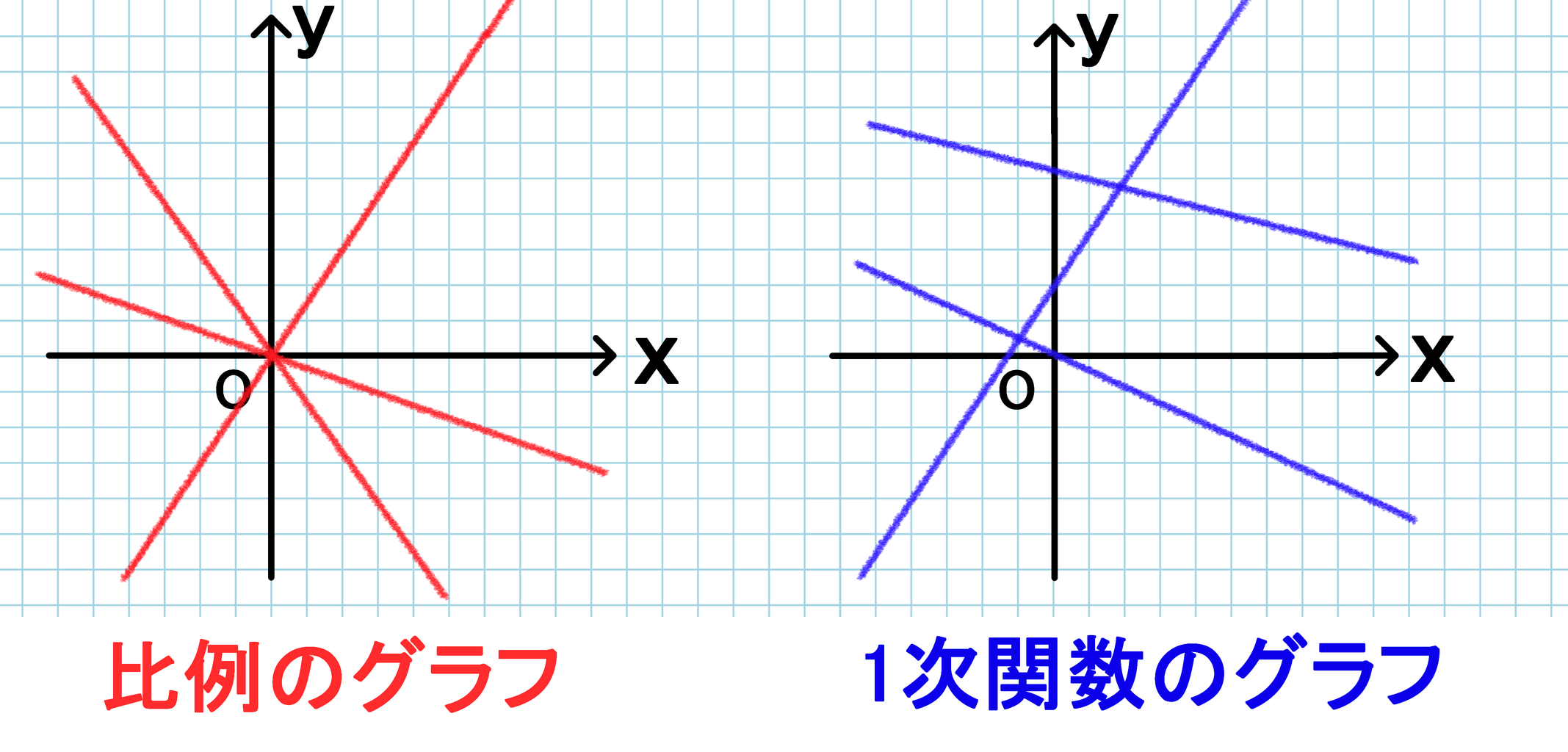



1次関数と比例の違いとは バカでもわかる 中学数学




中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




数学 中2 36 一次関数の交点をだす 基本編 Youtube




一次関数のグラフの利用1 無料で使える中学学習プリント
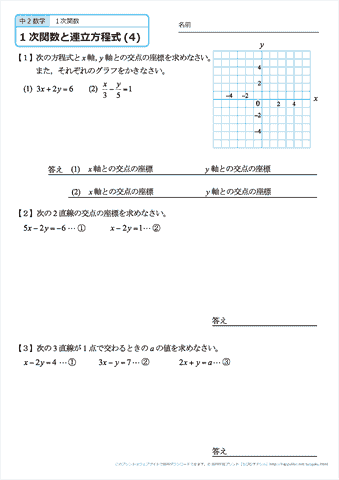



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
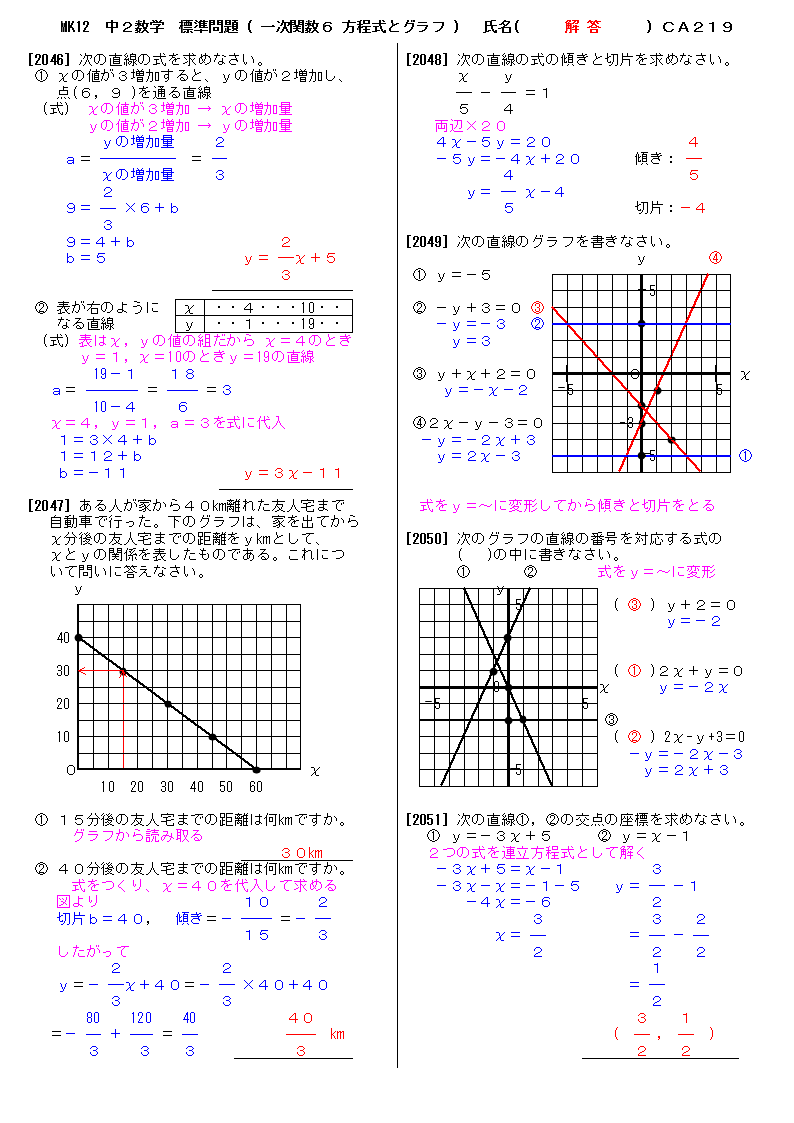



無料 中2数学 標準問題 解答プリント 219 一次関数6 方程式とグラフ



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




1 1 関数と方程式の違い Youtube



Http Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Yaruki Suugaku Documents M07 Pdf



Math 超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 働きアリ



中2数学 一次関数のグラフの書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1
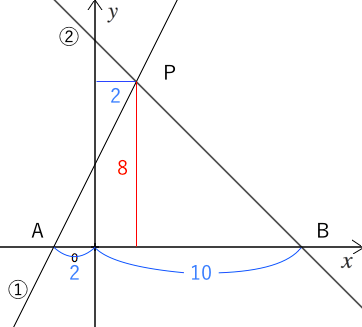



一次関数の利用 2直線が交わる 苦手な数学を簡単に




中学校数学 2年生 数量 一次関数 Wikibooks




数学 一次関数 中学生 数学のノート Clear




一次関数とは 式とグラフの解説 数学fun
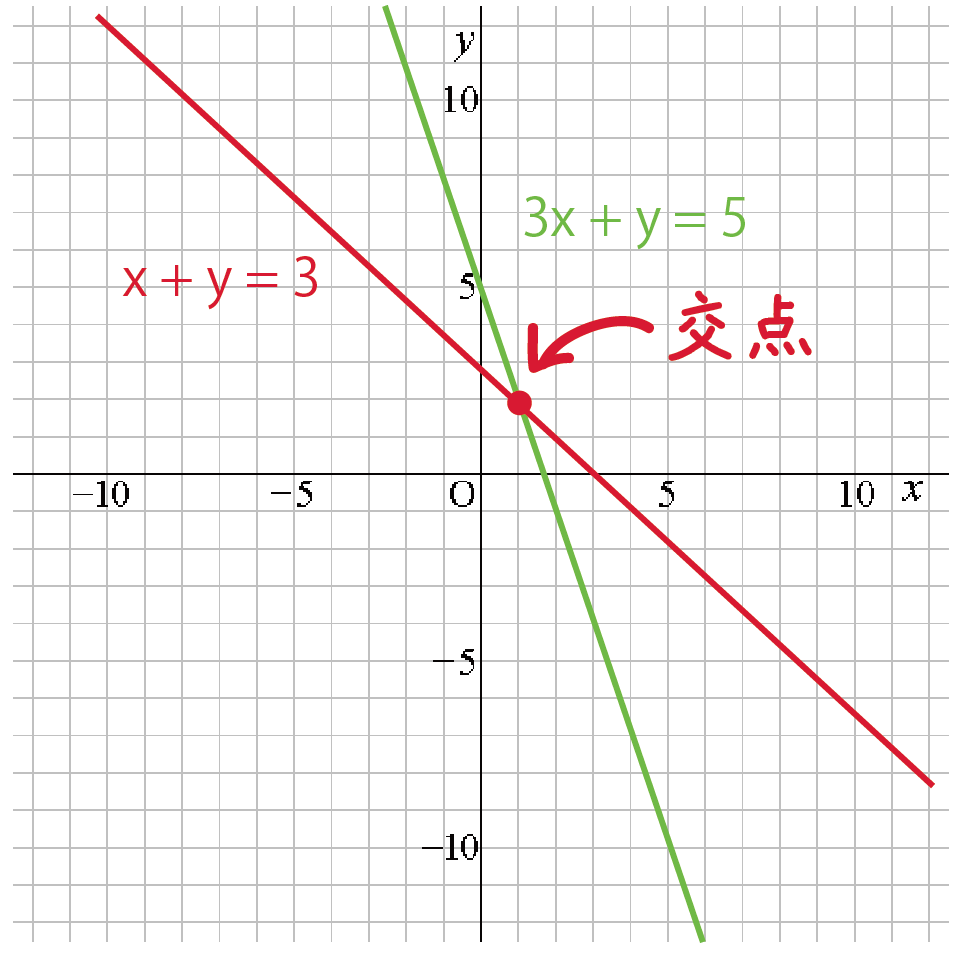



一次関数 グラフから連立方程式の解を求める3つのステップ Qikeru 学びを楽しくわかりやすく




Mathematics 1次関数 6 応用問題の解き方 1 1次関数と図形 働きアリ
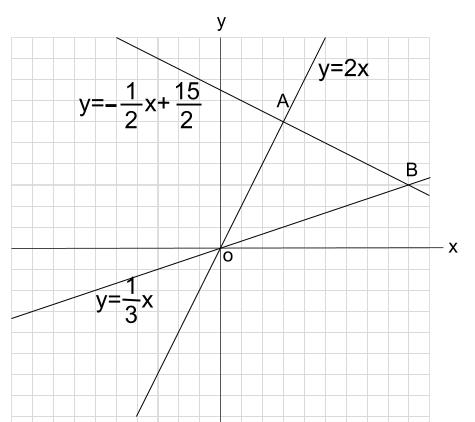



中学数学 1次関数と三角形の面積 その2 中学数学の無料オンライン学習サイトchu Su




こんな風に なぜ連立方程式で交点がわかるんですか Clear
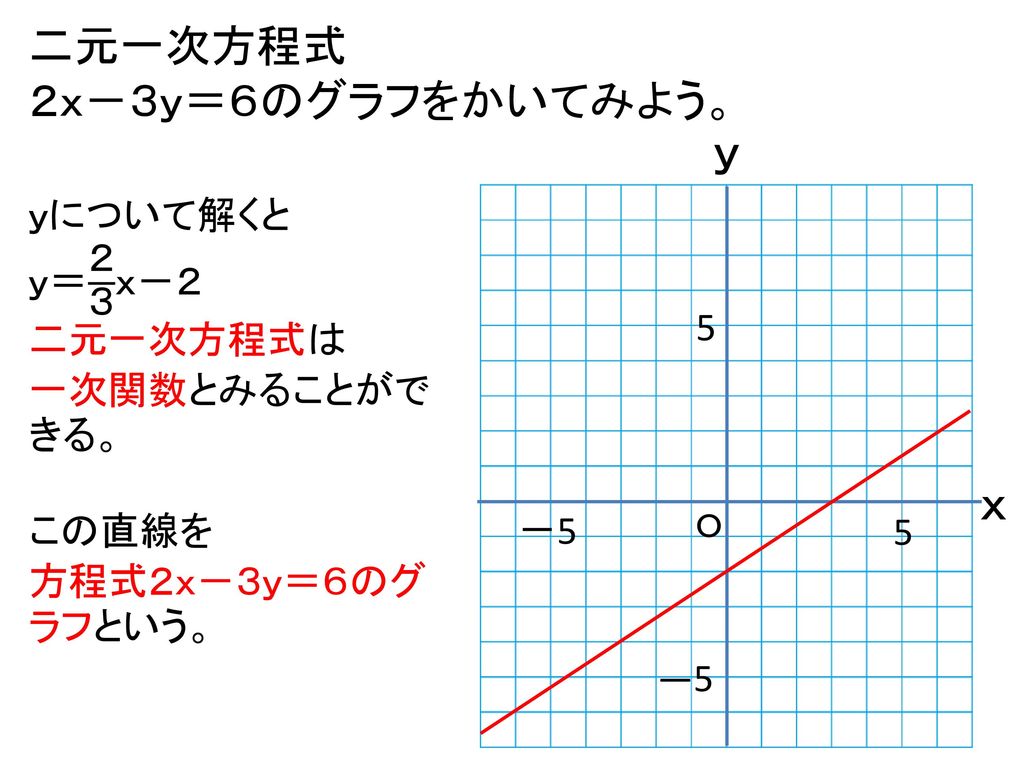



一次関数と方程式 本時の流れ ねらい 二元一次方程式をグラフに表すことができる 課題の提示 Yについて解き グラフをかく Ppt Download




切片が分からないときの一次関数の式の求め方 チーム エン
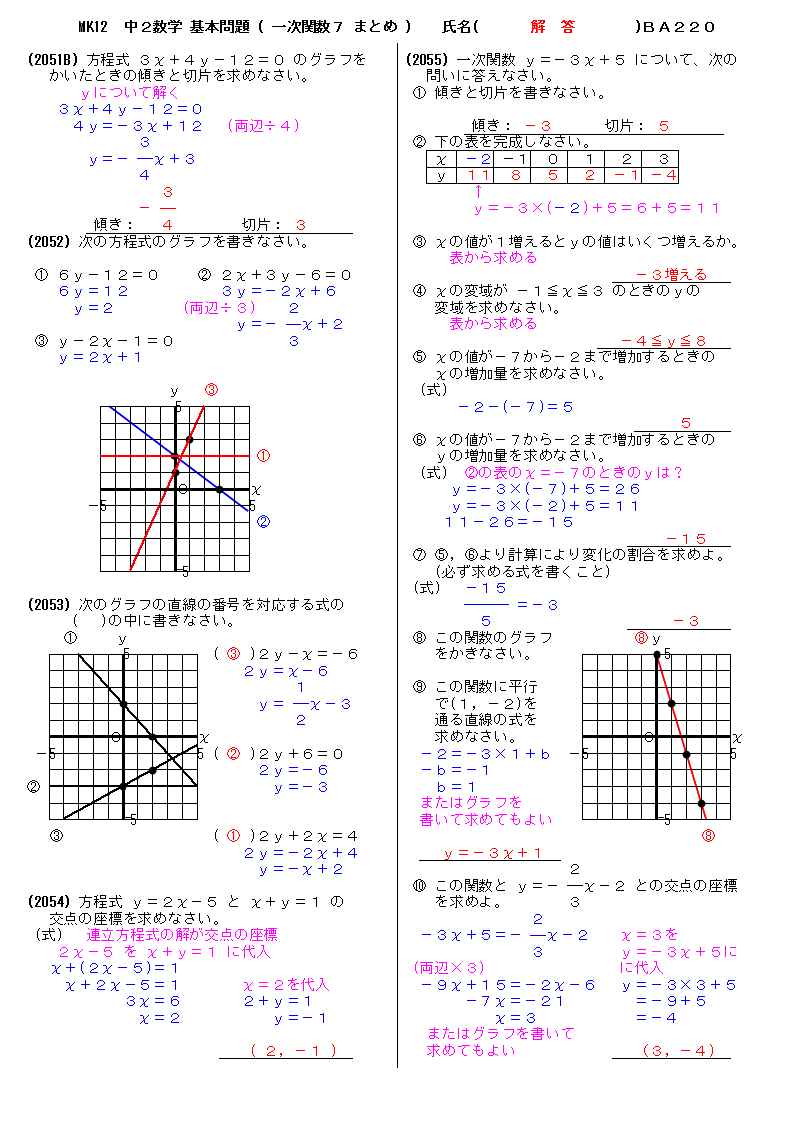



無料 中2数学 基本問題 解答プリント 2 一次関数7 まとめ



1




中学2年生 一次関数 連立方程式の解をグラフを使って求める問題です 4 5 のグ Clear
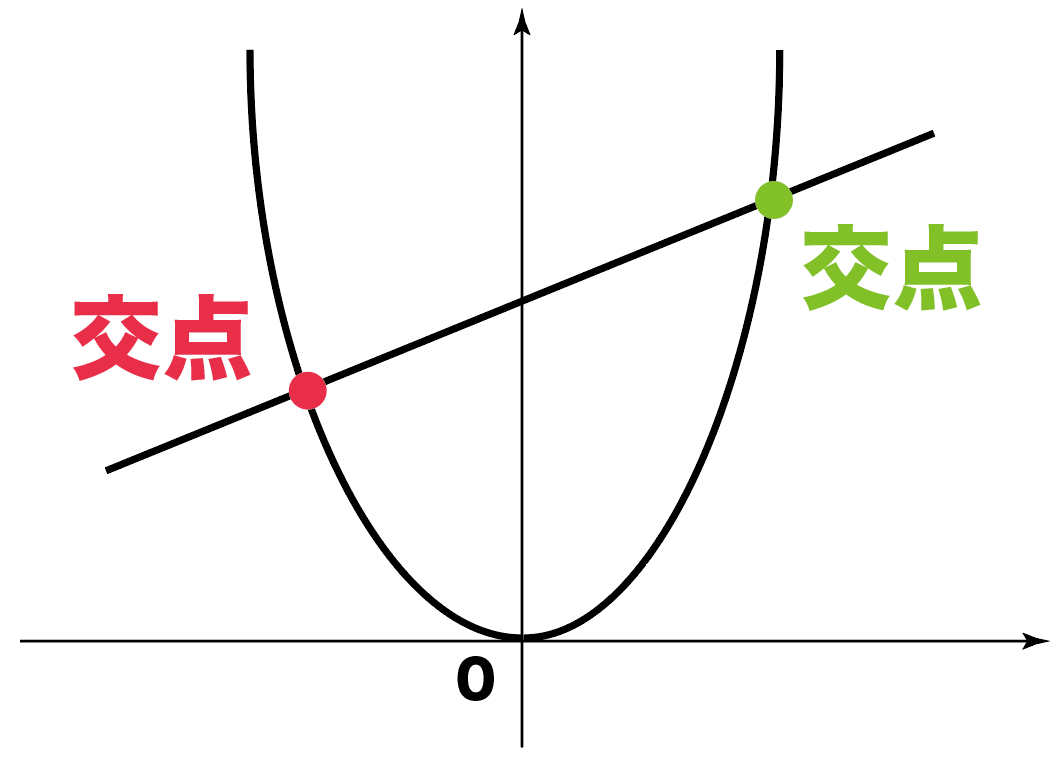



一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



1



一次関数とは グラフの書き方や一次関数の利用問題の解き方 受験辞典




1次関数と2元1次方程式の違い Youtube
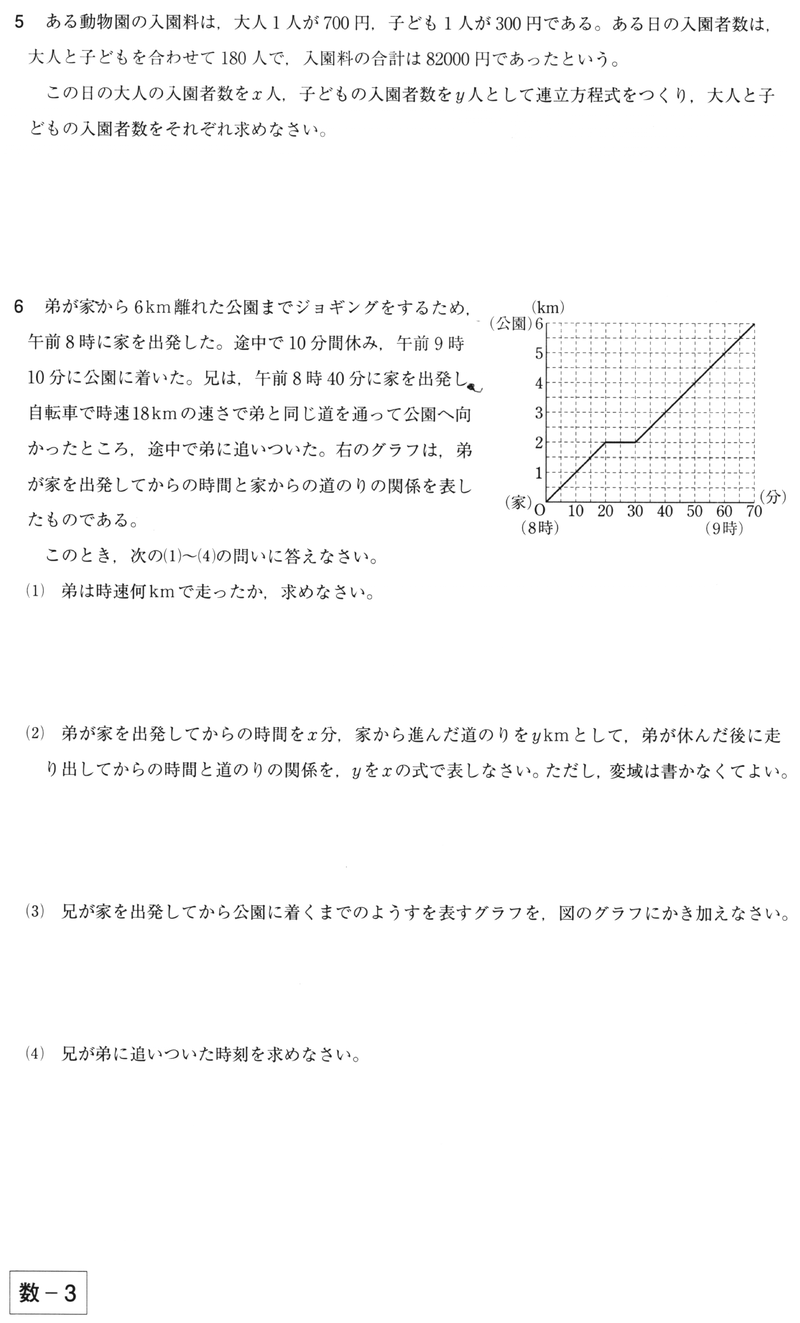



中学 数学 実力テスト 過去問 連立方程式 1次関数の利用 問題と解答 赤城 ᐡᐤᐡ
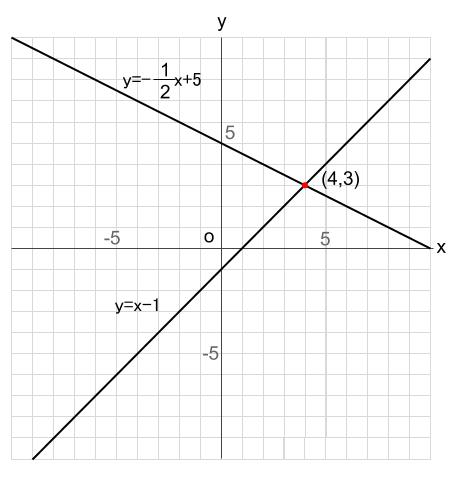



中学数学 2直線の交点 連立方程式とグラフ 中学数学の無料オンライン学習サイトchu Su




Excel エクセルで一次関数を計算し グラフを作る方法 一次関数の解を求める方法




中2数学 一次関数と方程式 二元一次方程式グラフの書き方 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



中2 1次関数4
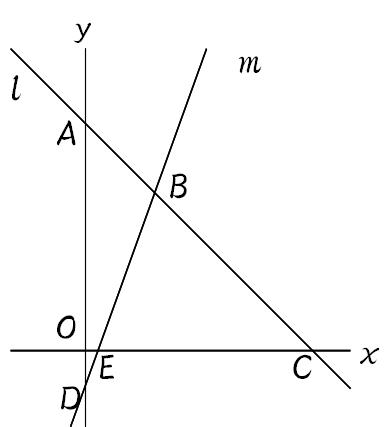



Mathematics 1次関数 6 応用問題の解き方 1 1次関数と図形 働きアリ




1次方程式と1次関数 数学i フリー教材開発コミュニティ Ftext




一次関数 2点を通る直線の式の求め方をイチから解説 Youtube
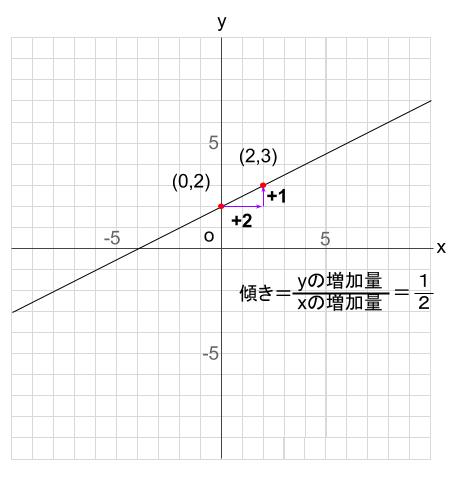



中学数学 1次関数 グラフの読み取り 中学数学の無料オンライン学習サイトchu Su




1次関数3 1次関数のグラフの交点と連立方程式の解 身勝手な主張
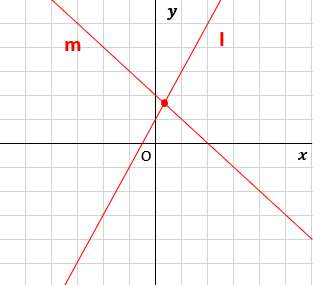



中2数学 一次関数と方程式 2直線の交点の座標の求め方 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




一次関数と方程式 本時の流れ ねらい 二元一次方程式をグラフに表すことができる 課題の提示 Yについて解き グラフをかく Ppt Download




一次関数 連立方程式とグラフの関係 苦手な数学を簡単に
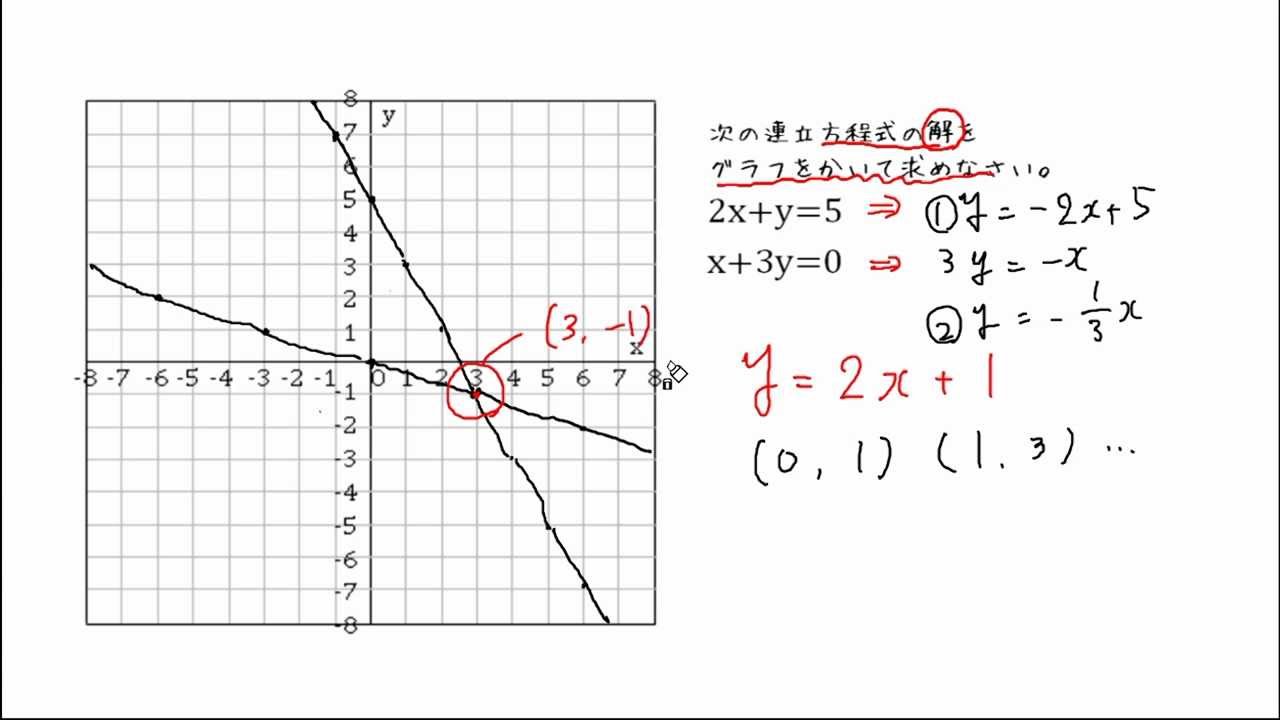



一次関数と連立方程式 Youtube
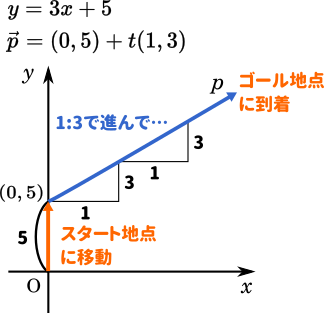



ベクトル方程式と媒介変数表示の仕組み やってることは一次関数と同じ Mm参考書




一次関数の応用問題 動く点p チーム エン




一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ



1次関数 グラフ 直線の方程式



超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 Shun Ei Note
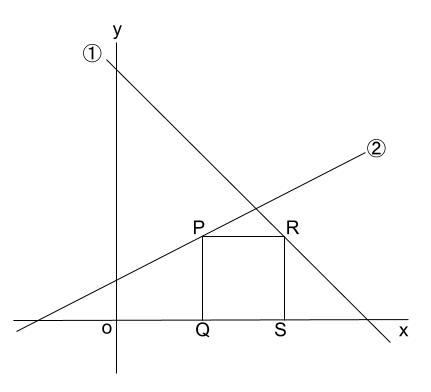



1次関数と正方形 中学数学の無料オンライン学習サイトchu Su



中2 1次関数4




次の条件を満たす一次関数の式を求めなさい Clear




1次関数 1次関数の式の求め方 中学数学 定期テスト対策サイト




方程式と関数の違いを理解しよう 理系のための備忘録
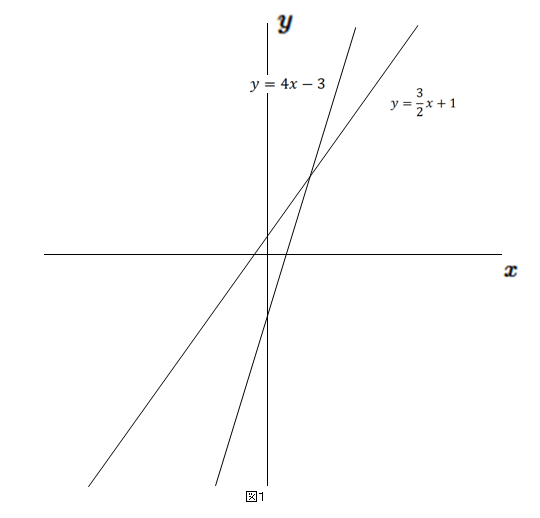



一次関数と連立方程式 2 ネット塾




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




一次関数 グラフから連立方程式の解を求める3つのステップ Qikeru 学びを楽しくわかりやすく
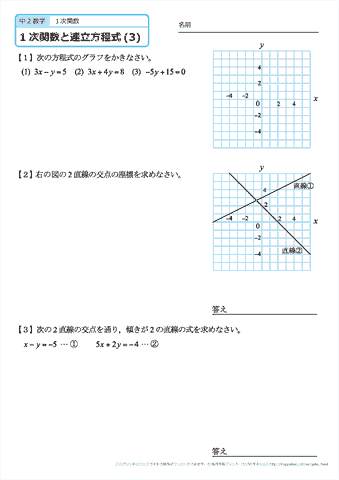



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




一次関数 表から式を求めるやり方についてイチから解説 Youtube




超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 Shun Ei Note
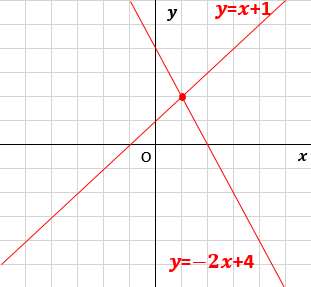



中2数学 一次関数と方程式 グラフの交点から連立方程式の解を求める 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



連立方程式と一次関数 名古屋市北区の学習塾は思考力を育む 泰成スクール


